ГДЗ по Математике 6 Класс Номер 146 Дорофеев, Шарыгин — Подробные Ответы

Исследуем.
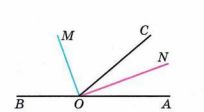
1) Рассмотрите рисунок 2.9: углы ВОС и СОА составляют развёрнутый угол, луч ОМ — биссектриса угла СОВ, луч ON — биссектриса угла АОС. Пусть угол AOC = 40 градусов. Чему равен угол между биссектрисами?
2) Решите эту же задачу при условии, что угол AOC равен 60 градусов; 82 градуса.
3) Какое можно выдвинуть предположение на основе решения этих задач? Попробуйте обосновать свой вывод.

1) Так как \(\angle AOC = 40^\circ\), а \(ON\) — биссектриса, то \(\angle CON = 40:2 = 20^\circ\). Углы \(\angle BOC\) и \(\angle AOC\) смежные, значит \(\angle BOC = 180^\circ — 40^\circ = 140^\circ\). Так как \(OM\) — биссектриса угла \(\angle BOC\), то \(\angle COM = 140:2 = 70^\circ\). Тогда \(\angle MON = \angle COM + \angle CON = 70^\circ + 20^\circ = 90^\circ\).

2) При \(\angle AOC = 60^\circ\): \(\angle CON = 60:2 = 30^\circ\); \(\angle BOC = 180^\circ — 60^\circ = 120^\circ\); \(\angle COM = 120:2 = 60^\circ\); \(\angle MON = 60^\circ + 30^\circ = 90^\circ\).

При \(\angle AOC = 82^\circ\): \(\angle CON = 82:2 = 41^\circ\); \(\angle BOC = 180^\circ — 82^\circ = 98^\circ\); \(\angle COM = 98:2 = 49^\circ\); \(\angle MON = 49^\circ + 41^\circ = 90^\circ\).

3) Угол между биссектрисами смежных углов равен \(90^\circ\).

1) Рассмотрим сначала заданный угол \(\angle AOC\). По условию \(\angle AOC = 40^\circ\), а луч \(ON\) является биссектрисой этого угла. Биссектриса делит угол на два равных угла, поэтому каждый из образовавшихся углов равен половине исходного: \(\angle CON = 40:2 = 20^\circ\). Далее используем свойство смежных углов: сумма смежных углов равна \(180^\circ\). Углы \(\angle AOC\) и \(\angle BOC\) смежные, поэтому \(\angle BOC = 180^\circ — \angle AOC = 180^\circ — 40^\circ = 140^\circ\). Теперь рассмотрим биссектрису \(OM\) угла \(\angle BOC\). Поскольку \(OM\) делит \(\angle BOC\) на два равных угла, получаем \(\angle COM = 140:2 = 70^\circ\). Чтобы найти угол между биссектрисами \(OM\) и \(ON\), нужно найти угол \(\angle MON\). Этот угол состоит из двух смежащихся частей: \(\angle COM\) и \(\angle CON\), так как обе части расположены между лучами \(OM\) и \(ON\) через луч \(OC\). Поэтому \(\angle MON = \angle COM + \angle CON = 70^\circ + 20^\circ = 90^\circ\). Таким образом, при \(\angle AOC = 40^\circ\) угол между биссектрисами смежных углов равен \(90^\circ\).

2) Теперь проделаем те же рассуждения для другого значения угла \(\angle AOC\). Пусть \(\angle AOC = 60^\circ\). Так как \(ON\) — биссектриса этого угла, то \(\angle CON = 60:2 = 30^\circ\). Углы \(\angle AOC\) и \(\angle BOC\) по-прежнему смежные, следовательно их сумма равна \(180^\circ\), откуда \(\angle BOC = 180^\circ — 60^\circ = 120^\circ\). Луч \(OM\) — биссектриса угла \(\angle BOC\), поэтому \(\angle COM = 120:2 = 60^\circ\). Как и в предыдущем случае, угол между биссектрисами равен сумме углов, которые они образуют с общим лучом \(OC\): \(\angle MON = \angle COM + \angle CON = 60^\circ + 30^\circ = 90^\circ\). Таким образом, и при \(\angle AOC = 60^\circ\) угол между биссектрисами смежных углов снова оказывается прямым.

Рассмотрим еще один вариант: \(\angle AOC = 82^\circ\). Луч \(ON\) делит этот угол пополам, поэтому каждая половина равна \(82:2 = 41^\circ\); следовательно, \(\angle CON = 41^\circ\). Как и прежде, воспользуемся тем, что углы \(\angle AOC\) и \(\angle BOC\) смежные: \(\angle BOC = 180^\circ — 82^\circ = 98^\circ\). Биссектриса \(OM\) делит угол \(\angle BOC\) пополам, значит \(\angle COM = 98:2 = 49^\circ\). Угол между биссектрисами \(OM\) и \(ON\) на рисунке снова получается как сумма углов \(\angle COM\) и \(\angle CON\): \(\angle MON = 49^\circ + 41^\circ = 90^\circ\). Мы видим, что при трех разных значениях исходного угла \(\angle AOC\) (40°, 60°, 82°) результат один и тот же: угол между биссектрисами смежных углов постоянен и равен \(90^\circ\).

3) На основе выполненных вычислений можно сделать обобщенный вывод. Пусть имеется развернутый угол, образованный лучами \(OB\) и \(OA\), то есть \(\angle BOA = 180^\circ\). Любой луч \(OC\) внутри этого развернутого угла разбивает его на два смежных угла: \(\angle BOC\) и \(\angle COA\), которые в сумме дают \(180^\circ\). Если провести биссектрису одного из углов, например \(\angle BOC\), получим луч \(OM\), делящий этот угол на два равных: \(\angle BOM = \angle COM\). Аналогично, биссектриса второго смежного угла \(\angle COA\) (луч \(ON\)) делит его на два равных: \(\angle CON = \angle NOA\). При этом можно показать, что сумма углов \(\angle COM\) и \(\angle CON\) всегда будет равна половине суммы смежных углов, то есть половине от \(180^\circ\). Действительно, так как \(\angle BOC + \angle COA = 180^\circ\), то после деления каждого угла пополам получаем два угла, лежащие между биссектрисами, суммарная величина которых равна \(\frac{180^\circ}{2} = 90^\circ\). Поэтому независимо от того, какой именно угол \(\angle AOC\) мы возьмем, угол между биссектрисами смежных углов всегда будет прямым: \(\angle MON = 90^\circ\).