ГДЗ по Математике 6 Класс Номер 145 Дорофеев, Шарыгин — Подробные Ответы

Анализируем и рассуждаем.
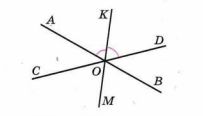
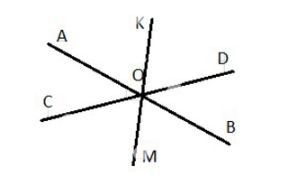
Начертите на листе нелинованной бумаги две пересекающиеся прямые АВ и CD. Точку пересечения прямых обозначьте буквой О. Постройте с помощью транспортира луч ОК — биссектрису угла AOD. Проведите луч ОМ, дополняющий луч ОК до прямой (рис. 2.8). Верно ли, что луч ОМ — биссектриса угла СОВ? Обоснуйте свой ответ.

Луч \(ОМ\) является биссектрисой угла \(СОВ\), так как:

\(-\angle AOD = \angle COB\) — как вертикальные;

\(-\angle AOK = \angle MOB\) — как вертикальные;

\(-\angle KOD = \angle COM\) — как вертикальные.

Значит, \(\angle COM = \angle MOB\), следовательно, \(ОМ\) — биссектриса \(\angle COB\).

Сначала рассмотрим пары вертикальных углов. Вертикальные углы образуются при пересечении двух прямых и всегда равны. В данной задаче известно, что лучи исходят из точки \(O\), а прямые пересекаются так, что образуются углы \(\angle AOD\), \(\angle COB\), \(\angle AOK\), \(\angle MOB\), \(\angle KOD\), \(\angle COM\). Так как \(\angle AOD\) и \(\angle COB\) являются вертикальными, то по свойству вертикальных углов они равны: \(\angle AOD = \angle COB\). Аналогично, углы \(\angle AOK\) и \(\angle MOB\) тоже вертикальные, поэтому \(\angle AOK = \angle MOB\). Третья пара вертикальных углов: \(\angle KOD\) и \(\angle COM\), следовательно, \(\angle KOD = \angle COM\).

Теперь проследим, как это связано с биссектрисой угла \(COB\). Биссектриса угла — это луч, который делит угол на два равных угла. Нам нужно показать, что луч \(OM\) делит угол \(COB\) на два равных угла, то есть что \(\angle COM = \angle MOB\). Из равенств вертикальных углов мы уже знаем: \(\angle AOK = \angle MOB\) и \(\angle KOD = \angle COM\). При этом все углы строятся вокруг точки \(O\), а лучи расположены так, что угол \(AOK\) является продолжением угла \(KOD\) на одной прямой, а угол \(MOB\) является продолжением угла \(COM\) на другой прямой. То есть углы \(\angle AOK\) и \(\angle KOD\) дополняют друг друга до развернутого угла, и то же самое верно для \(\angle COM\) и \(\angle MOB\).

Поскольку вертикальные углы по парам равны, мы фактически получаем равенство соответствующих частей угла \(COB\), отложенных по разные стороны от луча \(OM\). А именно, равенство \(\angle KOD = \angle COM\) показывает, что величина угла между лучами \(OC\) и \(OM\) совпадает с величиной угла между лучами, симметрично расположенными к ним на пересекающейся прямой. Равенство \(\angle AOK = \angle MOB\) показывает то же самое для другой части. В совокупности из этих равенств следует, что луч \(OM\) делит угол \(COB\) на два равных угла: \(\angle COM = \angle MOB\). Следовательно, по определению биссектрисы, луч \(OM\) является биссектрисой угла \(COB\).