ГДЗ по Математике 6 Класс Номер 14 Дорофеев, Шарыгин — Подробные Ответы

Запишите координаты каждой точки, отмеченной на координатной прямой (рис. 1.2).

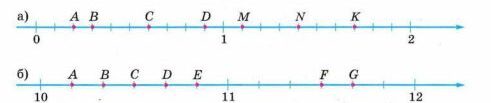
a) A \(\left(\frac{2}{10}\right)\); B \(\left(\frac{3}{10}\right)\); C \(\left(\frac{6}{10}\right)\); D \(\left(\frac{9}{10}\right)\); M \(\left(1\frac{1}{10}\right)\); N \(\left(1\frac{4}{10}\right)\); K \(\left(1\frac{7}{10}\right)\).

б) A \(\left(10\frac{1}{6}\right)\); B \(\left(10\frac{2}{6}\right)\); C \(\left(10\frac{3}{6}\right)\); D \(\left(10\frac{4}{6}\right)\); E \(\left(10\frac{5}{6}\right)\); F \(\left(11\frac{3}{6}\right)\); G \(\left(11\frac{4}{6}\right)\).

a)
Для каждого пункта требуется записать координату точки, используя дроби и смешанные числа. Например, точка \(A\) имеет координату \(\left(\frac{2}{10}\right)\), что означает, что она находится на расстоянии две десятых от нуля. Аналогично, точка \(B\) имеет координату \(\left(\frac{3}{10}\right)\), то есть три деления из десяти между нулём и единицей. Точка \(C\) расположена в точке \(\left(\frac{6}{10}\right)\), то есть на шести десятых отрезка между нулём и единицей. Точка \(D\) — в точке \(\left(\frac{9}{10}\right)\), то есть почти у самой единицы.

Далее идут точки, координаты которых выражены в виде смешанных чисел. Например, точка \(M\) имеет координату \(\left(1\frac{1}{10}\right)\), что означает, что она находится на одну целую и одну десятую от начала отсчёта, то есть чуть дальше единицы. Точка \(N\) имеет координату \(\left(1\frac{4}{10}\right)\), то есть одна целая и четыре десятых. Точка \(K\) — это \(\left(1\frac{7}{10}\right)\), то есть одна целая и семь десятых. Такие записи позволяют точно определить местоположение каждой точки на числовой прямой.

В итоге, для пункта a правильная запись координат всех точек будет следующей:
A \(\left(\frac{2}{10}\right)\);
B \(\left(\frac{3}{10}\right)\);
C \(\left(\frac{6}{10}\right)\);
D \(\left(\frac{9}{10}\right)\);
M \(\left(1\frac{1}{10}\right)\);
N \(\left(1\frac{4}{10}\right)\);
K \(\left(1\frac{7}{10}\right)\).

б)
Во втором пункте координаты точек выражаются через смешанные числа с дробной частью, где знаменатель равен шести. Например, точка \(A\) имеет координату \(\left(10\frac{1}{6}\right)\), что означает десять целых и одна шестая. Точка \(B\) — это \(\left(10\frac{2}{6}\right)\), то есть десять целых и две шестых. Точка \(C\) — \(\left(10\frac{3}{6}\right)\), то есть десять целых и три шестых. Точка \(D\) находится в точке \(\left(10\frac{4}{6}\right)\), а точка \(E\) — в точке \(\left(10\frac{5}{6}\right)\).

Далее идут точки, координаты которых лежат уже за десятью целыми, например, точка \(F\) — \(\left(11\frac{3}{6}\right)\), то есть одиннадцать целых и три шестых. Точка \(G\) — \(\left(11\frac{4}{6}\right)\), то есть одиннадцать целых и четыре шестых. Такие записи позволяют точно определить положение каждой точки на числовой прямой, даже если оно находится за пределами десятого деления.

В итоге для пункта б правильная запись координат всех точек будет следующей:
A \(\left(10\frac{1}{6}\right)\);
B \(\left(10\frac{2}{6}\right)\);
C \(\left(10\frac{3}{6}\right)\);
D \(\left(10\frac{4}{6}\right)\);
E \(\left(10\frac{5}{6}\right)\);
F \(\left(11\frac{3}{6}\right)\);
G \(\left(11\frac{4}{6}\right)\).