
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 138 Дорофеев, Шарыгин — Подробные Ответы
Работаем с символами.
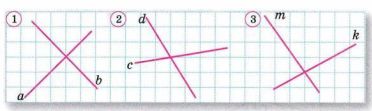
На каком из рисунков изображены перпендикулярные прямые (рис. 2.6)? Запишите факт перпендикулярности прямых, используя знак перпендикулярности.
Рассмотрим три рисунка:
- На рисунке 1 (a и b) — две прямые пересекаются под прямым углом, то есть они перпендикулярны.
- На рисунке 2 (c и d) — две прямые пересекаются, но угол между ними явно не прямой, значит, они не перпендикулярны.
- На рисунке 3 (m и k) — две прямые тоже пересекаются не под прямым углом, они не перпендикулярны.
Ответ: Перпендикулярные прямые изображены только на рисунке 1.
Запишем факт перпендикулярности, используя соответствующий символ:
a ⊥ b
Рассмотрим все три рисунка из задания:
- Рисунок 1. Здесь изображены две прямые: a и b. Они пересекаются под углом, который выглядит как прямой (90°). Значит, эти прямые перпендикулярны. Это можно узнать по тому, что угол между ними образует квадратную клетку тетради, а их пересечение делит клетку на четыре равные части.
- Рисунок 2. На этом рисунке изображены две прямые: c и d. Они пересекаются, но угол между ними заметно меньше прямого. Следовательно, прямые c и d не являются перпендикулярными.
- Рисунок 3. Здесь также две прямые: m и k. Угол между ними острый, значительно меньше 90°. Поэтому и эти прямые не перпендикулярны.
Вывод: Только на рисунке 1 прямые a и b пересекаются под прямым углом, то есть они перпендикулярны.
Факт перпендикулярности принято обозначать специальным знаком (⊥), который читается как «перпендикулярно».
Запишем это так:
a ⊥ b
Это запись читается: «прямая a перпендикулярна прямой b».
На остальных рисунках перпендикулярности нет, потому что угол между прямыми не является прямым.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!