Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 137 Дорофеев, Шарыгин — Подробные Ответы
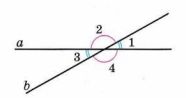
На рисунке 2.5 изображены две пересекающиеся прямые a и b. Найдите величины трёх других углов, если:
a) угол 1 = 29 градусов;
б) угол 4 = 137 градусов.
На рисунке изображены две пересекающиеся прямые a и b. Найдите величины трёх других углов, если:
а) угол 1 = 29°
- Углы 1 и 3 — вертикальные, значит, угол 3 = угол 1 = 29°.
- Углы 1 и 2 — смежные, их сумма 180°:
180° − 29° = 151° (это угол 2). - Углы 2 и 4 — вертикальные, значит, угол 4 = угол 2 = 151°.
Ответ: угол 2 = 151°, угол 3 = 29°, угол 4 = 151°.
б) угол 4 = 137°
- Угол 2 = угол 4 (вертикальные) ⇒ угол 2 = 137°.
- Угол 3 смежен с углом 4, их сумма 180°:
180° − 137° = 43° (это угол 3). - Угол 1 = угол 3 (вертикальные) ⇒ угол 1 = 43°.
Ответ: угол 1 = 43°, угол 2 = 137°, угол 3 = 43°.
На рисунке 2.5 изображены две пересекающиеся прямые a и b. Найдите величины трёх других углов, если:
а) угол 1 = 29°
- Рассмотрим углы, образованные при пересечении двух прямых. Здесь каждая пара противоположных (вертикальных) углов равна.
- Угол 3 — вертикальный по отношению к углу 1. По свойству вертикальных углов: угол 3 = угол 1.
Угол 3 = 29°. - Углы 1 и 2 — смежные. По свойству смежных углов, их сумма равна 180°:
угол 1 + угол 2 = 180°.
Значит, угол 2 = 180° − угол 1 = 180° − 29° = 151°. - Угол 4 вертикален углу 2, значит угол 4 = угол 2 = 151°.
Итак, если угол 1 = 29°, то:
угол 2 = 151°, угол 3 = 29°, угол 4 = 151°.
б) угол 4 = 137°
- Снова используем свойства вертикальных и смежных углов.
- Угол 2 — вертикальный к углу 4, значит угол 2 = угол 4 = 137°.
- Угол 3 смежный с углом 4, их сумма 180°:
угол 3 = 180° − угол 4 = 180° − 137° = 43°. - Угол 1 вертикален углу 3, поэтому угол 1 = угол 3 = 43°.
Итак, если угол 4 = 137°, то:
угол 1 = 43°, угол 2 = 137°, угол 3 = 43°.
Пояснения:
— Вертикальные углы — это пары углов, которые лежат напротив друг друга при пересечении двух прямых; они всегда равны.
— Смежные углы — это пары углов, у которых одна сторона общая, а две другие продолжают друг друга в прямую; сумма смежных углов всегда равна 180°.
— Зная один угол, можно найти все остальные с помощью этих свойств.
