ГДЗ по Математике 6 Класс Номер 136 Дорофеев, Шарыгин — Подробные Ответы

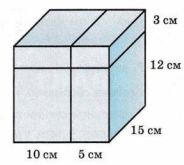
Куб с ребром 15 см рассекли двумя разрезами, как показано на рисунке 1.21. Сколько получилось частей? Найдите объём каждой части.

Куб имеет ребро \(15\) см. Первый разрез делит основание на части шириной \(10\) см и \(5\) см, второй разрез делит высоту на части \(12\) см и \(3\) см, значит получаем \(2 \cdot 2 = 4\) части.

Первая часть: размеры \(10\), \(12\), \(15\), объём \(V_1 = 10 \cdot 12 \cdot 15 = 1800\ \text{см}^3\).

Вторая часть: размеры \(5\), \(3\), \(15\), объём \(V_2 = 5 \cdot 3 \cdot 10 = 450\ \text{см}^3\).

Третья часть: размеры \(15\), \(3\), \(5\), объём \(V_3 = 15 \cdot 3 \cdot 5 = 225\ \text{см}^3\).

Четвёртая часть: размеры \(15\), \(5\), \(12\), объём \(V_4 = 15 \cdot 5 \cdot 12 = 900\ \text{см}^3\).

Куб имеет ребро \(15\) см, то есть его размеры по длине, ширине и высоте равны \(15\) см. На рисунке показано, что куб разрезали двумя плоскостями. Первая плоскость вертикальная: она делит нижнее ребро на отрезки \(10\) см и \(5\) см, то есть по горизонтали куб разбивается на две части с основаниями \(10 \times 15\) и \(5 \times 15\). Вторая плоскость горизонтальная: она делит высоту куба на отрезки \(12\) см и \(3\) см, то есть по вертикали куб разбивается на нижнюю часть высотой \(12\) см и верхнюю часть высотой \(3\) см. Так как одна плоскость делит на \(2\) части и другая тоже на \(2\) части, в итоге получаем \(2 \cdot 2 = 4\) части куба.

Рассмотрим размеры и объём каждой части. Первая часть \(V_1\) находится снизу слева: её ширина по основанию \(10\) см, высота \(12\) см, глубина (третье измерение куба) остаётся полной и равна \(15\) см. Объём прямоугольного параллелепипеда находится по формуле \(V = a \cdot b \cdot c\). Поэтому для первой части получаем \(V_1 = 10 \cdot 12 \cdot 15 = 10 \cdot 180 = 1800\ \text{см}^3\). Это самая большая часть, так как у неё и высота, и ширина берутся по большим отрезкам разрезов.

Вторая часть \(V_2\) находится сверху слева: её ширина такая же, как у первой части, \(10\) см, но высота уже верхняя, то есть только \(3\) см, глубина также \(15\) см. Тогда объём второй части равен \(V_2 = 10 \cdot 3 \cdot 15 = 30 \cdot 15 = 450\ \text{см}^3\). Третья часть \(V_3\) находится сверху справа: ширина по основанию теперь \(5\) см (меньшая часть после вертикального разреза), высота \(3\) см (верхняя часть после горизонтального разреза), глубина снова \(15\) см. Следовательно, её объём \(V_3 = 5 \cdot 3 \cdot 15 = 15 \cdot 15 = 225\ \text{см}^3\).

Четвёртая часть \(V_4\) располагается снизу справа: её ширина по основанию \(5\) см, высота нижняя \(12\) см, глубина \(15\) см. Объём этой части вычисляется как \(V_4 = 5 \cdot 12 \cdot 15 = 60 \cdot 15 = 900\ \text{см}^3\). Если сложить объёмы всех четырёх частей, получим \(V_1 + V_2 + V_3 + V_4 = 1800 + 450 + 225 + 900 = 3375\ \text{см}^3\). Это совпадает с объёмом всего исходного куба \(15^3 = 3375\ \text{см}^3\), что подтверждает правильность разбиения и вычислений.