ГДЗ по Математике 6 Класс Номер 1054 Дорофеев, Шарыгин — Подробные Ответы
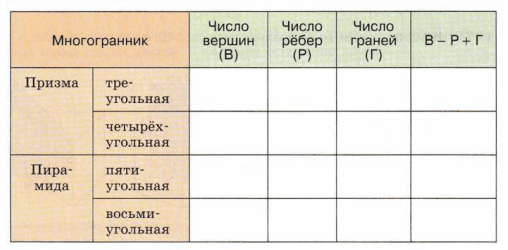
Исследуем. Пусть в многограннике В — число вершин, Р — число рёбер и Г — число граней. Число В — Р + Г называют эйлеровой характеристикой, по имени великого математика Леонарда Эйлера. Убедитесь, что для всех многогранников в таблице это число равно 2, т.е. В — Р + Г = 2.
Многогранник Число вершин (В) Число рёбер (Р) Число граней (Г) В — Р + Г
Призма
треугольная
четырёхугольная
Пирамида
пятиугольная
восьмиугольная
| Многогранник | (В) | (Р) | (Г) | В – Р + Г |
|---|---|---|---|---|
| 3-угольная призма | 6 | 9 | 5 | 6 – 9 + 5 = 5 – 3 = 2 |
| 4-угольная призма | 8 | 12 | 6 | 8 – 12 + 6 = 6 – 4 = 2 |
| 5-угольная пирамида | 6 | 10 | 6 | 6 – 10 + 6 = 6 – 4 = 2 |
| 8-угольная пирамида | 9 | 16 | 9 | 9 – 16 + 9 = 9 – 7 = 2 |
Утверждение В – Р + Г = 2 — верно.
Где:
В — число вершин,
Р — число рёбер,
Г — число граней.
Это соотношение называется формулой Эйлера для выпуклого многогранника и подтверждается на примерах в таблице для разных типов призм и пирамид.
| Многогранник | (В) — вершин | (Р) — рёбер | (Г) — граней | В – Р + Г |
|---|---|---|---|---|
| 3-угольная призма | 6 | 9 | 5 | 6 – 9 + 5 = 5 – 3 = 2 |
| 4-угольная призма | 8 | 12 | 6 | 8 – 12 + 6 = 6 – 4 = 2 |
| 5-угольная пирамида | 6 | 10 | 6 | 6 – 10 + 6 = 6 – 4 = 2 |
| 8-угольная пирамида | 9 | 16 | 9 | 9 – 16 + 9 = 9 – 7 = 2 |
Пояснения к формуле и примерам:
В данной таблице показаны разные многогранники — призмы и пирамиды, и для каждого из них указано количество вершин (В), рёбер (Р) и граней (Г). Для каждого многогранника проводится вычисление по формуле В – Р + Г. Это известная формула Эйлера для выпуклых многогранников.
- Для 3-угольной призмы:
- Вершин 6 (по 3 на каждом основании),
- рёбер 9 (3 внизу, 3 вверху и 3 боковых),
- граней 5 (2 основания и 3 боковые грани).
- Подставляем: 6 – 9 + 5 = 2. Формула верна.
- Для 4-угольной призмы:
- Вершин 8 (по 4 на каждом основании),
- рёбер 12 (4 внизу, 4 вверху и 4 боковых),
- граней 6 (2 основания и 4 боковые грани).
- Подставляем: 8 – 12 + 6 = 2. Формула верна.
- Для 5-угольной пирамиды:
- Вершин 6 (5 вершин основания и одна вершина — вершина пирамиды),
- рёбер 10 (5 в основании и 5 рёбер, соединяющих вершину пирамиды с вершинами основания),
- граней 6 (5 треугольных боковых и 1 основание).
- Подставляем: 6 – 10 + 6 = 2. Формула верна.
- Для 8-угольной пирамиды:
- Вершин 9 (8 в основании и одна вершина пирамиды),
- рёбер 16 (8 в основании и 8 боковых),
- граней 9 (8 треугольных боковых и 1 основание).
- Подставляем: 9 – 16 + 9 = 2. Формула верна.
Таким образом, во всех примерах выполняется равенство В – Р + Г = 2, что подтверждает справедливость формулы Эйлера для выпуклых многогранников. Это одно из фундаментальных утверждений геометрии, используемое для проверки правильности построения или анализа свойств многогранников.
