ГДЗ по Математике 6 Класс Номер 1053 Дорофеев, Шарыгин — Подробные Ответы

Наблюдаем и анализируем.
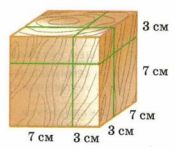
Куб сребром 10 см распилили на части тремя плоскостями, параллельными его граням, так, как показано на рисунке 12.42. На сколько частей разрезали куб? Найдите объёмы наибольшей и наименьшей получившихся частей.

Куб разрезали на 8 частей.

Объем наибольшей части равен:

7 · 7 · 7 = 49 · 7 = 343 (см³).

Объем наименьшей части равен:

3 · 3 · 3 = 27 (см³).

Ответ: 343 см³; 27 см³.

Куб разрезали на 8 частей.

Задача состоит в том, чтобы найти объем самой большой и самой маленькой части, на которые был разделён куб. Для этого сначала определяем размеры каждой части и подставляем их в формулу объема куба, где объем рассчитывается как произведение длины, ширины и высоты.

Объем наибольшей части равен:

7 × 7 × 7 = 49 × 7 = 343 (см³).

Наибольшая часть получилась, если все её стороны равны 7 см. Тогда объем считается по формуле: V = 7 × 7 × 7 = 343 см³. Это максимальный объем среди всех частей, на которые был разрезан куб.

Объем наименьшей части равен:

3 × 3 × 3 = 27 (см³).

Наименьшая часть получилась, если все её стороны равны 3 см. Соответственно, объем считается по формуле: V = 3 × 3 × 3 = 27 см³. Это минимальный объем среди всех частей.

Ответ: 343 см³; 27 см³.