ГДЗ по Математике 6 Класс Номер 1051 Дорофеев, Шарыгин — Подробные Ответы
Работаем с символами.
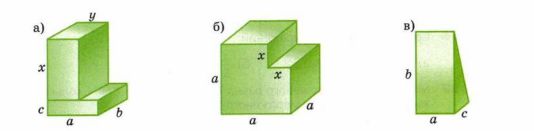
Запишите формулу для вычисления объёма V многогранника (рис. 12.41, а-в).
а) V = xyb + abc.
б) V = a³ — ax².
в) V = ½ abc.
а) V = xyb + abc.
Эта формула выражает объем некоторой геометрической фигуры, который складывается из двух слагаемых: произведения x, y и b, а также произведения a, b и c. В такой формуле x, y, a, b, c могут быть длинами сторон, высотами, ширинами или другими размерами фигуры. Чаще всего такие выражения встречаются, если фигура состоит из двух частей или комбинации двух объемов.
б) V = a³ — ax².
Данная формула может описывать объем сложной фигуры, у которой из одного объема (например, куба со стороной a) вычитается объем другой фигуры (например, призмы или цилиндра с основанием ax²). a³ — это объем куба со стороной a, а ax² — это объем призмы с основанием x² и высотой a. Итоговый объем равен разности этих двух фигур.
в) V = ½ abc.
Эта формула часто используется для вычисления объема треугольной призмы, где основание — треугольник с площадью (½ ab), а высота призмы равна c. В общем случае, ½ abc — это объем, если площадь основания равна половине произведения двух сторон, а c — высота. Формула показывает, что чтобы найти объем такой призмы, нужно вычислить площадь основания и умножить на высоту.
