Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 1045 Дорофеев, Шарыгин — Подробные Ответы
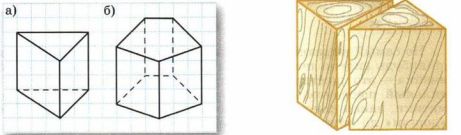
а) Куб распилили, как показано на рисунке 12.38. Какие при этом получились многогранники?
б) Нарисуйте пятиугольную призму (например, как на рисунке 12.37, б). Покажите, как можно распилить её на треугольные призмы.
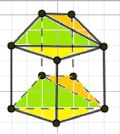
a) Если куб распилить, как показано на рисунке, то получатся две треугольные призмы.
б) Например, распилим так:
а) Если куб распилить, как показано на рисунке, то получатся две треугольные призмы.
Куб — это многогранник, все грани которого являются квадратами. Если распилить его вдоль одной из диагонал, то получится две треугольные призмы. Каждая из них будет иметь треугольную форму основания и прямоугольные боковые грани. Эти призмы будут одинаковыми по форме и размерам, так как распил происходит вдоль диагонали, что обеспечивает симметричность.
Для этого мы должны распилить куб вдоль одной из его диагонал, и каждая часть, полученная после разреза, будет представлять собой треугольную призму, основание которой — равнобедренный треугольник.
б) Например, распилим так:
Если распилим куб по диагонали его основания, то получится две призмы с одинаковыми треугольными основаниями. Каждый разрез будет проходить через центр основания и вершины куба. Таким образом, каждое основание будет равнобедренным треугольником, а боковые грани — прямоугольными.
Данный способ распила используется для создания фигур, которые будут иметь одинаковые треугольные основания, и это особенно важно в задачах, связанных с объемами и поверхностями многогранников.
