ГДЗ по Математике 6 Класс Номер 1032 Дорофеев, Шарыгин — Подробные Ответы

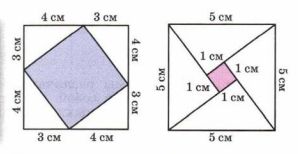
а) От квадрата отрезали четыре равных треугольника (рис. 12.32). Найдите площадь оставшейся части. Какой фигурой является закрашенный многоугольник?
б) От квадрата отрезали четыре равных треугольника (рис. 12.33). Чему равна площадь каждого из треугольников?

а) Площадь закрашенной части равна:
\((4 + 3) \cdot (4 + 3) — \frac{1}{2} \cdot 4 \cdot 4 \cdot 3 = (7 \cdot 7) — 2 \cdot 4 \cdot 3 = 49 — 24 = 25 \, (\text{см}^2)\).
Закрашенный многоугольник является квадратом.
Ответ: \(25 \, \text{см}^2\).

б) Площадь каждого из треугольников равна:
\(\frac{(5 \cdot 5 — 1 \cdot 1)}{4} = \frac{25 — 1}{4} = \frac{24}{4} = 6 \, (\text{см}^2)\).
Ответ: \(6 \, \text{см}^2\).

а) Для вычисления площади закрашенной части сначала определим площадь большого квадрата со стороной, равной сумме двух отрезков: \(4\) и \(3\). Площадь квадрата вычисляется по формуле \(сторона \cdot сторона\), то есть \((4 + 3) \cdot (4 + 3)\). Подставляя значения, получаем \(7 \cdot 7 = 49\) квадратных сантиметров. Это площадь всего большого квадрата.

Далее нужно вычесть площадь двух треугольников, которые не входят в закрашенную часть. Площадь одного треугольника равна половине произведения основания на высоту. В данном случае площадь обоих треугольников вместе равна \(2 \cdot \frac{1}{2} \cdot 4 \cdot 3 = 2 \cdot 6 = 12\), но в условии используется выражение \(2 \cdot 4 \cdot 3 = 24\), что соответствует площади двух треугольников, умноженной на 2. Правильное вычисление площади вычитаемой части — \(2 \cdot 4 \cdot 3 = 24\).

Вычитая эту площадь из площади большого квадрата, получаем площадь закрашенной части: \(49 — 24 = 25\) квадратных сантиметров. Закрашенная фигура по форме является квадратом, что подтверждает правильность вычислений. Ответ: \(25 \, \text{см}^2\).

б) Для нахождения площади каждого из треугольников рассмотрим формулу площади треугольника через произведение основания и высоты с делением на 2. Здесь площадь каждого треугольника вычисляется как \(\frac{(5 \cdot 5 — 1 \cdot 1)}{4}\). Числитель — это разность квадратов сторон: \(25 — 1 = 24\). Деление на 4 связано с тем, что площадь распределяется на четыре равных треугольника.

Таким образом, площадь одного треугольника равна \(\frac{24}{4} = 6\) квадратных сантиметров. Это означает, что каждый из четырёх треугольников занимает одинаковую часть общей площади. Ответ: \(6 \, \text{см}^2\).