ГДЗ по Математике 6 Класс Номер 1031 Дорофеев, Шарыгин — Подробные Ответы

Найдите площадь закрашенного треугольника (рис. 12.31).

1) Площадь прямоугольника:
\(5 \cdot 6 = 30\) (кв. ед).

2) Площадь первого прямоугольного треугольника:
\(\frac{1}{2} \cdot 3 \cdot 6 = \frac{1}{2} \cdot 18 = 9\) (кв. ед).

3) Площадь второго прямоугольного треугольника:
\(\frac{1}{2} \cdot 2 \cdot 5 = \frac{1}{2} \cdot 10 = 5\) (кв. ед).

4) Площадь третьего прямоугольного треугольника:
\(\frac{1}{2} \cdot 1 \cdot 5 = \frac{1}{2} \cdot 5 = 2{,}5\) (кв. ед).

5) Площадь закрашенного треугольника:
\(30 — (9 + 5 + 2{,}5) = 30 — 16{,}5 = 13{,}5\) (кв. ед).

Ответ: 13,5 кв. ед.

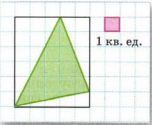
1) Для начала вычислим площадь всего прямоугольника. Из условия известно, что длина прямоугольника равна 5 единиц, а ширина — 6 единиц. Площадь прямоугольника находится по формуле произведения длины на ширину, то есть \(5 \cdot 6\). Выполним умножение: \(5 \cdot 6 = 30\). Значит, площадь всего прямоугольника составляет 30 квадратных единиц.

2) Далее найдем площадь первого прямоугольного треугольника. Для этого используем формулу площади треугольника: половина произведения основания на высоту. Основание первого треугольника равно 3, а высота — 6. Значит, площадь равна \(\frac{1}{2} \cdot 3 \cdot 6\). Сначала умножим 3 на 6, получим 18, затем разделим на 2: \(\frac{18}{2} = 9\). Таким образом, площадь первого треугольника равна 9 квадратных единиц.

3) Теперь вычислим площадь второго прямоугольного треугольника. Его основание равно 2, а высота — 5. По формуле площади треугольника получаем: \(\frac{1}{2} \cdot 2 \cdot 5\). Сначала перемножим 2 и 5, получим 10, затем разделим на 2: \(\frac{10}{2} = 5\). Значит, площадь второго треугольника равна 5 квадратных единиц.

4) Площадь третьего прямоугольного треугольника найдем аналогично. Основание равно 1, высота — 5. Подставляем в формулу: \(\frac{1}{2} \cdot 1 \cdot 5\). Перемножаем 1 и 5, получаем 5, делим на 2: \(\frac{5}{2} = 2{,}5\). Так что площадь третьего треугольника равна 2,5 квадратных единиц.

5) Чтобы найти площадь закрашенного треугольника, нужно из площади всего прямоугольника вычесть площади трёх прямоугольных треугольников. Складываем площади треугольников: \(9 + 5 + 2{,}5 = 16{,}5\). Теперь вычитаем из площади прямоугольника: \(30 — 16{,}5 = 13{,}5\). Следовательно, площадь закрашенного треугольника равна 13,5 квадратных единиц.

Ответ: 13,5 кв. ед.