Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 1030 Дорофеев, Шарыгин — Подробные Ответы
Анализируем и рассуждаем.
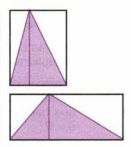
Прямоугольники, изображённые на рисунке 12.30, равновелики. Верно ли, что закрашенные треугольники также имеют одинаковые площади?
Так как прямоугольники равновелики, а площади закрашенных треугольников равны половине площадей прямоугольников, то закрашенные треугольники так же имеют одинаковые площади.
В данной задаче рассматривается важное свойство прямоугольников и прямоугольных треугольников. Прямоугольники являются равновеликими, что означает, что они имеют одинаковые площади, если их размеры (длина и ширина) одинаковы. Следовательно, все прямоугольники с одинаковыми размерами будут иметь одинаковую площадь.
Далее рассматриваются закрашенные треугольники, которые образованы в каждом прямоугольнике. Площадь прямоугольного треугольника равна половине площади соответствующего прямоугольника, так как прямоугольный треугольник занимает половину пространства прямоугольника, деленного на два равных треугольника.
Таким образом, если прямоугольники равны по площади, то и их половины — закрашенные треугольники — также будут иметь одинаковую площадь. Это логически вытекает из того, что площадь каждого прямоугольного треугольника составляет половину площади прямоугольника, а значит, все закрашенные треугольники, образованные одинаковыми прямоугольниками, будут равными по площади.
Итак, если прямоугольники равновелики, то и закрашенные треугольники, которые составляют половину площади этих прямоугольников, будут иметь одинаковые площади.
