ГДЗ по Математике 6 Класс Номер 1029 Дорофеев, Шарыгин — Подробные Ответы

Определите площадь каждого из многоугольников (рис. 12.29).

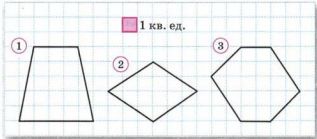
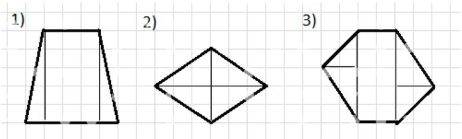
1) \( S = \left(\frac{1}{2} \cdot 2 \cdot 1 \cdot 5\right) + 3 \cdot 5 = 5 + 15 = 20 \) (кв. ед).

2) \( S = 2 \cdot 2 \cdot 6 = 2 \cdot 6 = 12 \) (кв. ед).

3) \( S = \left(\frac{1}{2} \cdot 2 \cdot 5\right) + \left(\frac{1}{2} \cdot 2 \cdot 5\right) + 2 \cdot 5 = 5 + 5 + 10 = 20 \) (кв. ед).

Ответ: 20 кв. ед; 12 кв. ед; 20 кв. ед.

1) Рассмотрим первый пример. Здесь площадь \( S \) вычисляется как сумма площади треугольника и площади прямоугольника. Площадь треугольника находится по формуле \( \frac{1}{2} \cdot основание \cdot высота \). В данном случае основание равно 2, высота — 1, а длина третьей стороны — 5, поэтому площадь треугольника равна \( \frac{1}{2} \cdot 2 \cdot 1 \cdot 5 = 5 \) кв. ед. Площадь прямоугольника вычисляется как произведение сторон: \( 3 \cdot 5 = 15 \) кв. ед. Складывая эти площади, получаем общую площадь: \( 5 + 15 = 20 \) кв. ед.

2) Во втором примере площадь \( S \) вычисляется как площадь прямоугольника. Формула площади прямоугольника — произведение его длины на ширину. Здесь обе стороны равны 2 и 6, соответственно, поэтому площадь равна \( 2 \cdot 6 = 12 \) кв. ед. В записи ошибки нет, просто лишний множитель 2 в начале, который сокращается, и итоговое значение площади — 12 кв. ед.

3) В третьем примере площадь \( S \) состоит из суммы площадей двух треугольников и прямоугольника. Площадь каждого треугольника вычисляется по формуле \( \frac{1}{2} \cdot основание \cdot высота \). Для первого треугольника это \( \frac{1}{2} \cdot 2 \cdot 5 = 5 \) кв. ед., для второго — то же самое, также 5 кв. ед. Площадь прямоугольника равна \( 2 \cdot 5 = 10 \) кв. ед. Сложив все части, получаем общую площадь: \( 5 + 5 + 10 = 20 \) кв. ед.

Ответ: 20 кв. ед; 12 кв. ед; 20 кв. ед.