
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 1028 Дорофеев, Шарыгин — Подробные Ответы
1) Можно найти площадь прямоугольника и вычесть площади прямоугольных треугольников:
\(6 \cdot 4 — \frac{1}{2} \cdot (4 \cdot 4 + 2 \cdot 4) = 24 — \frac{1}{2} \cdot (16 + 8) = 24 — \frac{1}{2} \cdot 24 = 24 — 12 = 12\) (кв. ед).
2) Можно найти площади двух прямоугольных треугольников и сложить их площади:
\(\frac{1}{2} \cdot (4 \cdot 4 + 4 \cdot 2) = \frac{1}{2} \cdot (16 + 8) = \frac{1}{2} \cdot 24 = 12\) (кв. ед).
3) Значит, площадь треугольника можно найти по формуле:
\(S = \frac{1}{2} a h = \frac{1}{2} \cdot 6 \cdot 4 = 3 \cdot 4 = 12\) (кв. ед).
Ответ: 12 кв. ед.
1) Для начала рассмотрим первый способ нахождения площади треугольника. Мы берём прямоугольник, у которого длина равна 6, а ширина равна 4. Площадь прямоугольника вычисляется по формуле \(6 \cdot 4 = 24\) квадратных единиц. Однако внутри этого прямоугольника находятся два прямоугольных треугольника, площадь которых нужно вычесть. Площадь каждого прямоугольного треугольника вычисляется по формуле \( \frac{1}{2} \times \text{основание} \times \text{высота} \). В данном случае основания и высоты треугольников равны 4 и 4, а также 2 и 4. Складываем площади этих двух треугольников: \( \frac{1}{2} \cdot (4 \cdot 4 + 2 \cdot 4) = \frac{1}{2} \cdot (16 + 8) = \frac{1}{2} \cdot 24 = 12 \). Вычитаем эту сумму из площади прямоугольника: \(24 — 12 = 12\) квадратных единиц.
2) Второй способ заключается в том, чтобы сразу найти площади двух прямоугольных треугольников и сложить их. Для этого мы используем ту же формулу площади треугольника \( \frac{1}{2} \times \text{основание} \times \text{высота} \). Площадь первого треугольника равна \( \frac{1}{2} \cdot 4 \cdot 4 = 8 \), а второго — \( \frac{1}{2} \cdot 4 \cdot 2 = 4 \). Складываем эти площади: \(8 + 4 = 12\) квадратных единиц. Таким образом, площадь треугольника равна сумме площадей двух прямоугольных треугольников, что даёт нам тот же результат — 12 квадратных единиц.
3) Третий способ — это использование общей формулы площади треугольника \( S = \frac{1}{2} a h \), где \(a\) — основание, а \(h\) — высота треугольника. В нашем случае основание равно 6, а высота — 4. Подставляя эти значения, получаем: \( S = \frac{1}{2} \cdot 6 \cdot 4 = 3 \cdot 4 = 12 \) квадратных единиц. Этот способ является самым простым и универсальным, так как позволяет найти площадь треугольника напрямую, не разбивая его на части. Все три способа дают одинаковый результат, подтверждая правильность ответа.
Ответ: 12 кв. ед.


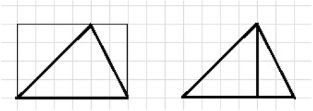


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!