ГДЗ по Математике 6 Класс Номер 1027 Дорофеев, Шарыгин — Подробные Ответы

Экспериментируем.
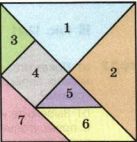
На рисунке 12.27 изображена древняя китайская головоломка «Тантрам».
1) Вырежите из бумаги квадрат со стороной 8 см и разрежьте его на фигуры танграма. Назовите все семь фигур. Есть ли среди них равные? Найдите площадь каждой фигуры. Назовите равновеликие фигуры.
2) Составьте:
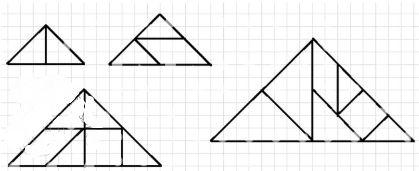
а) треугольник из двух, трёх, пяти и семи частей танграма;
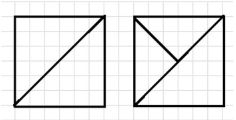
б) квадрат из двух и трёх частей танграма;
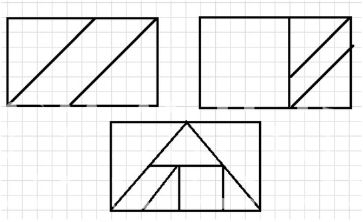
в) прямоугольник из трёх, четырёх и семи частей танграма.
3) Из каких частей танграма можно составить:
а) две равные фигуры;
б) две равновеликие фигуры;
в) прямоугольник, равновеликий треугольнику 7?

1) Фигуры 1 и 2 равны, так как оба — равнобедренные прямоугольные треугольники с одинаковыми катетами. Площадь \(1\) и \(2\):

\(S = \frac{1}{2}ab = \frac{1}{2} \cdot 8 \cdot 4 = 4 \cdot 4 = 16 \, (\text{см}^2)\).

2) Фигуры 3 и 5 равны, оба — равнобедренные прямоугольные треугольники с катетами 4 и 2. Площадь \(3\) и \(5\):

\(S = \frac{1}{2}ab = \frac{1}{2} \cdot 4 \cdot 2 = 4 \, (\text{см}^2)\).

3) Площадь фигуры 4 (квадрат):

\(S = S_3 \cdot 2 = 4 \cdot 2 = 8 \, (\text{см}^2)\).

4) Площадь фигуры 6 (параллелограмм):

\(S = ab = 4 \cdot 2 = 8 \, (\text{см}^2)\).

5) Площадь фигуры 7:

\(S = \frac{1}{2}ab = \frac{1}{2} \cdot 4 \cdot 4 = 2 \cdot 4 = 8 \, (\text{см}^2)\).

Равновеликие фигуры: 1 и 2; 3 и 5; 4, 6 и 7.

2) Равенство фигур:

а)

б)

в)

3) Составление фигур:

а) Две равные фигуры можно составить из:

• 3 треугольников, получим квадрат 4;
• 3 треугольника, получим треугольник 7.

б) Две равновеликие фигуры можно составить из:

• 3 треугольников, они будут равновелики фигуре 4, 6 или 7.

в) Прямоугольник, равновеликий треугольнику 7, можно составить из 3 и 5 треугольников.

1) Рассмотрим первые две фигуры, которые являются равнобедренными прямоугольными треугольниками. Они равны, так как у них одинаковые длины катетов — 8 см и 4 см. Площадь прямоугольного треугольника вычисляется по формуле \(S = \frac{1}{2}ab\), где \(a\) и \(b\) — катеты. Для фигуры 1 и 2 подставляем значения: \(S = \frac{1}{2} \cdot 8 \cdot 4 = 4 \cdot 4 = 16\) квадратных сантиметров. Это означает, что площадь обеих фигур одинакова и равна 16 см², что подтверждает их равенство по площади.

2) Следующие фигуры 3 и 5 также равнобедренные прямоугольные треугольники, но с катетами длиной 4 см и 2 см. Их площадь также вычисляется по той же формуле: \(S = \frac{1}{2}ab = \frac{1}{2} \cdot 4 \cdot 2 = 4\) см². Поскольку у них одинаковая площадь, эти фигуры равновелики, то есть имеют равные площади, несмотря на то, что размеры меньше, чем у фигур 1 и 2.

3) Фигура 4 — квадрат, площадь которого равна стороне в квадрате. В условии указано, что площадь квадрата равна удвоенной площади фигуры 3, то есть \(S_4 = S_3 \cdot 2 = 4 \cdot 2 = 8\) см². Таким образом, площадь квадрата равна 8 см². Это важно, потому что площадь квадрата совпадает с площадью параллелограмма (фигура 6) и равнобедренного прямоугольного треугольника (фигура 7).

4) Площадь фигуры 6, которая является параллелограммом, вычисляется по формуле \(S = ab\), где \(a\) и \(b\) — основания и высота. Подставляя значения, получаем \(S = 4 \cdot 2 = 8\) см². Это совпадает с площадью квадрата (фигура 4), что говорит о равенстве этих фигур по площади.

5) Последняя фигура 7 — равнобедренный прямоугольный треугольник с катетами 4 см и 4 см. Площадь вычисляется так: \(S = \frac{1}{2}ab = \frac{1}{2} \cdot 4 \cdot 4 = 2 \cdot 4 = 8\) см². Площадь совпадает с площадями фигур 4 и 6, что означает, что эти три фигуры равновелики.

Таким образом, равновеликими являются фигуры: 1 и 2 (площадь 16 см²), 3 и 5 (площадь 4 см²), а также 4, 6 и 7 (площадь 8 см²). Это показывает, что несмотря на различие форм, площади некоторых фигур совпадают, что важно для сравнения и анализа геометрических свойств.

2) Равенство фигур:

а)

б)

в)

3) Составление фигур:

а) Из трёх равных треугольников, например, 3, можно составить квадрат, равный фигуре 4. Также из трёх таких треугольников можно составить треугольник, равный фигуре 7.

б) Две равновеликие фигуры, например, треугольники 3 и 5, можно сложить, чтобы получить фигуру, равную по площади фигурам 4, 6 или 7.

в) Прямоугольник, равновеликий треугольнику 7, можно составить из треугольников 3 и 5, сложив их так, чтобы образовалась фигура с равной площадью.

Таким образом, изучение равенства фигур и их площадей позволяет не только сравнивать, но и составлять новые фигуры из данных, используя свойства треугольников, квадратов и параллелограммов.