Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 1025 Дорофеев, Шарыгин — Подробные Ответы
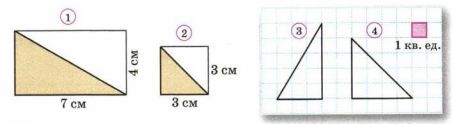
Чему равна площадь каждого треугольника (рис. 12.26)?
Указание. Достройте треугольник до прямоугольника.
Площадь прямоугольного треугольника будет равна половине площади прямоугольника.
1) 4 * 7 : 2 = 28 : 2 = 14 (см²).
2) 3 * 3 : 2 = 9 : 2 = 4,5 (см²).
3) 5 * 3 : 2 = 15 : 2 = 7,5 (кв. ед.).
4) 4 * 4 : 2 = 16 : 2 = 8 (кв. ед.).
Ответ: 14 см², 4,5 см², 7,5 кв. ед., 8 кв. ед.
Площадь прямоугольного треугольника будет равна половине площади прямоугольника.
В данной задаче рассматривается важное свойство прямоугольных треугольников. Площадь прямоугольного треугольника можно найти как половину площади прямоугольника, образованного теми же основаниями и высотами. Это связано с тем, что в прямоугольном треугольнике одна из сторон является основанием, а другая — высотой, и его площадь будет равна половине площади соответствующего прямоугольника.
1) Для первого примера давайте возьмем прямоугольник с длиной основания 4 см и высотой 7 см. Площадь этого прямоугольника вычисляется по формуле:
Площадь прямоугольника = основание * высота.
Итак, площадь прямоугольника равна:
4 * 7 = 28 (см²).
Теперь, так как площадь прямоугольного треугольника будет равна половине площади прямоугольника, получаем:
28 : 2 = 14 (см²).
Ответ: 14 см².
2) В следующем примере мы рассматриваем прямоугольник с основанием 3 см и высотой 3 см. Площадь прямоугольника вычисляется аналогично:
3 * 3 = 9 (см²).
Площадь прямоугольного треугольника будет равна половине площади прямоугольника:
9 : 2 = 4,5 (см²).
Ответ: 4,5 см².
3) Для третьего примера давайте возьмем прямоугольник с основанием 5 см и высотой 3 см. Площадь прямоугольника будет:
5 * 3 = 15 (кв. ед.).
Площадь прямоугольного треугольника, как и в предыдущих примерах, будет равна половине площади прямоугольника:
15 : 2 = 7,5 (кв. ед.).
Ответ: 7,5 кв. ед.
4) В последнем примере основание прямоугольника равно 4 см, а высота — 4 см. Площадь прямоугольника:
4 * 4 = 16 (кв. ед.).
Площадь прямоугольного треугольника:
16 : 2 = 8 (кв. ед.).
Ответ: 8 кв. ед.
Итоговый ответ: 14 см², 4,5 см², 7,5 кв. ед., 8 кв. ед.
