Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 1024 Дорофеев, Шарыгин — Подробные Ответы
1) а) Измерения прямоугольника равны 3 см и 4 см.
Площадь параллелограмма равна площади прямоугольника:
3 * 4 = 12 (см²).
б) Измерения прямоугольника равны 4 см и 5 см.
Площадь параллелограмма равна площади прямоугольника:
4 * 5 = 20 (см²).
Ответ: 12 см², 20 см².
2) Формула для вычисления площади параллелограмма:
S = a * h
1) а) Измерения прямоугольника равны 3 см и 4 см.
Для вычисления площади прямоугольника используется формула:
Площадь прямоугольника = длина * ширина.
В данном случае, длина прямоугольника равна 3 см, а ширина — 4 см. Таким образом, площадь прямоугольника будет равна:
3 * 4 = 12 (см²).
Площадь параллелограмма в данном случае будет такой же, так как параллелограмм с такими измерениями может быть равен прямоугольнику по площади, если его основание и высота совпадают с соответствующими размерами прямоугольника.
б) Измерения прямоугольника равны 4 см и 5 см.
Для второго случая площадь прямоугольника можно найти с помощью той же формулы:
Площадь прямоугольника = длина * ширина.
Длина прямоугольника равна 4 см, а ширина — 5 см. Следовательно, площадь прямоугольника будет равна:
4 * 5 = 20 (см²).
Площадь параллелограмма с такими размерами также будет равна площади прямоугольника, так как в данном случае параллелограмм и прямоугольник имеют одинаковое основание и высоту.
Ответ: 12 см², 20 см².
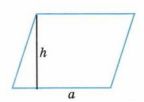
2) Формула для вычисления площади параллелограмма:
Площадь параллелограмма вычисляется по формуле:
S = a * h, где:
- a — основание параллелограмма (длина его одной стороны),
- h — высота, перпендикулярная к основанию.
Эта формула позволяет вычислить площадь параллелограмма, если известны его основание и высота.
