Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 1021 Дорофеев, Шарыгин — Подробные Ответы
Рассуждаем.
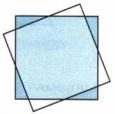
Два одинаковых квадрата расположены так, как показано на рисунке 12.21. Докажите, что сумма площадей синих треугольников равна сумме площадей белых треугольников.
Если один из квадратов повернуть вокруг центра симметрии, то оба квадрата совпадут, следовательно, треугольники равны, а значит и равны суммы их площадей.
Если один из квадратов повернуть вокруг центра симметрии, то оба квадрата совпадут. Это означает, что все стороны и углы одного квадрата будут точно совпадать с соответствующими сторонами и углами другого квадрата. Такой эффект возникает благодаря симметрии, которая сохраняет все пропорции фигуры при её вращении на 180 градусов.
Следовательно, поскольку оба квадрата совпадают, то и треугольники, полученные при делении каждого квадрата, также будут равны. Это происходит потому, что они будут иметь одинаковую форму и размер — их стороны и углы будут одинаковыми, а значит, их площади тоже будут одинаковыми.
Таким образом, мы можем утверждать, что суммы площадей двух таких равных треугольников, полученных из этих одинаковых квадратов, также будут равными. Площадь каждого квадрата делится на два равных треугольника, и, так как сами квадраты равны, сумма их площадей также будет одинаковой.
Итак, вращение одного квадрата вокруг его центра симметрии не изменяет его площади, а значит, равны и суммы площадей частей этих квадратов, например, треугольников, полученных при их разбиении.
