Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 1010 Дорофеев, Шарыгин — Подробные Ответы
Рассуждаем.
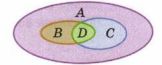
1) Пусть А — множество параллелограммов, В — множество прямоугольников, С-множество ромбов (рис. 12.14). Множество каких четырёхугольников обозначено буквой D?
2) Закончите предложение:
Всякий прямоугольник является … .
Всякий ромб является … .
Всякий квадрат является … .
1) D — множество квадратов.
2) Каждый прямоугольник является параллелограммом.
Каждый ромб является параллелограммом.
Каждый квадрат является параллелограммом, ромбом и прямоугольником.
1) D — множество квадратов.
Множество D состоит из всех возможных квадратов. Квадрат — это особый случай прямоугольника, у которого все стороны равны между собой, а углы прямые (90°). Множество квадратов включает все геометрические фигуры, которые соответствуют этим характеристикам, и объединяет их в одно множество. Каждый квадрат также является прямоугольником, ромбом и параллелограммом, так как все эти фигуры могут быть описаны через такие же геометрические свойства, как у квадрата.
2) Каждый прямоугольник является параллелограммом.
Прямоугольник — это четырёхугольник, у которого все углы прямые (90°), а противоположные стороны равны и параллельны. Следовательно, каждый прямоугольник является параллелограммом, так как параллелограмм определяется как четырёхугольник, у которого противоположные стороны параллельны и равны. У прямоугольника эти свойства выполняются, поэтому он также относится к классу параллелограммов.
Каждый ромб является параллелограммом.
Ромб — это четырёхугольник, у которого все стороны равны между собой, а противоположные углы равны. Ромб является частным случаем параллелограмма, поскольку его противоположные стороны параллельны. Таким образом, каждый ромб автоматически является параллелограммом, поскольку соответствует основным признакам параллелограмма — параллельности противоположных сторон и равенству противоположных углов.
Каждый квадрат является параллелограммом, ромбом и прямоугольником.
Квадрат — это геометрическая фигура, которая одновременно является прямоугольником, ромбом и параллелограммом. Все стороны квадрата равны, все углы прямые, а противоположные стороны параллельны. Таким образом, квадрат является частным случаем всех этих фигур. Он сочетает в себе свойства прямоугольника (углы 90°), ромба (все стороны равны) и параллелограмма (параллельность противоположных сторон). Поэтому каждый квадрат является одновременно прямоугольником, ромбом и параллелограммом.
