Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 1007 Дорофеев, Шарыгин — Подробные Ответы
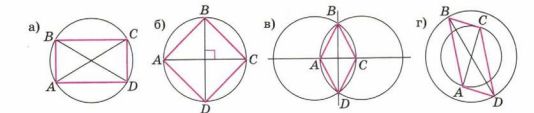
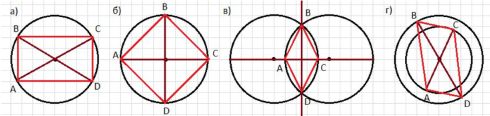
На рисунке 12.12, а-г показаны способы построения следующих четырёхугольников: прямоугольника, квадрата, ромба и параллелограмма. Опишите словами способ построения каждого четырёхугольника и выполните построения.
а) Рисуем окружность и проводим два диаметра. Соединяем последовательно точки пересечения диаметров с окружностью.
б) Рисуем окружность и проводим два диаметра, перпендикулярных друг другу. Соединяем последовательно точки пересечения диаметров с окружностью.
в) Строим две пересекающиеся окружности и через их центры проводим прямую. Проводим прямую через точки пересечения окружностей. Соединяем последовательно точки пересечения окружностей и точки пересечения окружности с прямой.
г) Строим две концентрические окружности. Проводим их диаметры и соединяем точки пересечения диаметров с окружностями последовательно.
а) Рисуем окружность и проводим два диаметра. Соединяем последовательно точки пересечения диаметров с окружностью.
Для выполнения первого этапа задания, начертим окружность с любым радиусом, используя циркуль. Затем проводим два диаметра. Диаметры — это прямые линии, которые проходят через центр окружности и соединяют противоположные точки на окружности. После того как два диаметра будут проведены, на каждой окружности будут образовываться две точки пересечения с этими диаметрами. Необходимо последовательно соединить эти точки, используя линейку, образуя дополнительные линии внутри окружности.
б) Рисуем окружность и проводим два диаметра, перпендикулярных друг другу. Соединяем последовательно точки пересечения диаметров с окружностью.
Во втором случае мы также начертим окружность. После этого необходимо провести два диаметра, которые должны быть перпендикулярны друг другу, то есть угол между ними должен быть 90°. Один диаметр будет горизонтальным, а другой — вертикальным. Эти диаметры будут пересекать окружность в четырёх точках. После этого соединяем последовательно точки пересечения этих диаметров с окружностью, получая несколько отрезков внутри окружности, которые пересекаются друг с другом.
в) Строим две пересекающиеся окружности и через их центры проводим прямую. Проводим прямую через точки пересечения окружностей.
На третьем шаге нам нужно построить две окружности, которые пересекаются друг с другом в одной точке. Для этого сначала рисуем одну окружность, затем рисуем вторую окружность так, чтобы они пересекались. Затем через их центры проводим прямую линию, которая будет проходить через обе окружности. Также необходимо провести прямую через точки пересечения этих окружностей. Соединяя эти точки, мы получаем интересные геометрические формы, такие как пересекающиеся линии и участки, ограниченные окружностями.
г) Строим две концентрические окружности. Проводим их диаметры и соединяем точки пересечения диаметров с окружностями последовательно.
Для последнего этапа строим две концентрические окружности, то есть окружности, которые имеют общий центр, но разные радиусы. После этого проводим два диаметра для каждой окружности. Диаметры будут пересекать каждую окружность в противоположных точках. Необходимо соединить точки пересечения этих диаметров с каждой окружностью. При этом важно отметить, что из-за одинакового центра этих окружностей все полученные линии будут иметь определённую симметрию, создавая интересные геометрические фигуры.
