ГДЗ по Математике 6 Класс Номер 1002 Дорофеев, Шарыгин — Подробные Ответы
Экспериментируем.
Диагонали прямоугольника равны, а диагонали квадрата не только равны, но и перпендикулярны друг другу.
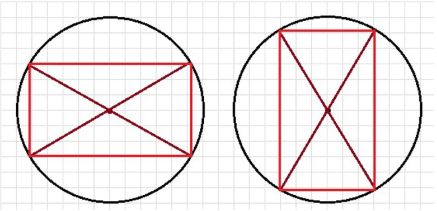
а) Постройте прямоугольник, диагонали которого равны 6 см. Постройте другой прямоугольник с такими же диагоналями.
б) Постройте квадрат с диагоналями, равными 8 см. Можно ли построить ещё один квадрат с такими же диагоналями?
а) Строим окружность с диаметром 6 см. Проводи два диаметра и соединяем точки пересечения последовательно:
Для выполнения этого задания, начертим окружность с центром в точке и диаметром 6 см. После этого проведем два диаметра, которые будут пересекать окружность в её центре. Затем соединяем точки пересечения этих диаметров с окружностью, образуя отрезки, которые будут пересекаться внутри окружности.
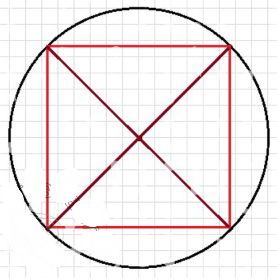
б) Квадрат, с диагоналями, равными 8 см, можно построить только один:
Для построения квадрата с диагоналями, равными 8 см, начертим квадрат, где каждая диагональ будет равна 8 см. С помощью линейки измеряем 8 см для диагоналей, и, используя эти диагонали, строим квадрат. Этот квадрат можно построить только один, так как для заданной длины диагоналей существует только одно возможное расположение квадратных сторон.
а) Строим окружность с диаметром 6 см. Проводи два диаметра и соединяем точки пересечения последовательно:
Для выполнения этого задания начертим окружность с центром в точке. Окружность должна иметь диаметр 6 см, что означает радиус равный 3 см. После того как окружность будет нарисована, проведем два диаметра, которые будут пересекать окружность в её центре. Диаметры должны быть прямыми линиями, соединяющими противоположные точки окружности и проходящими через её центр. Эти два диаметра могут располагаться под разными углами, но в любом случае они будут делить окружность на четыре равные части. Затем мы соединяем точки пересечения этих диаметров с окружностью, образуя несколько отрезков внутри окружности. Эти отрезки и диагонали будут пересекаться в центре окружности и образовывать несколько различных фигур внутри круга, таких как ромб или другие геометрические формы.
б) Квадрат, с диагоналями, равными 8 см, можно построить только один:
Для построения квадрата, у которого диагонали равны 8 см, следует помнить, что диагонали квадрата всегда пересекаются в его центре под прямым углом, и они делят квадрат на четыре равных треугольника. Для начала нарисуйте одну диагональ длиной 8 см, используя линейку. Затем, на этой диагонали найдите её середину (это будет центр квадрата). Теперь, проведите вторую диагональ, которая также должна быть длиной 8 см, и обязательно перпендикулярно первой диагонали. Таким образом, мы получаем квадрат, где диагонали равны 8 см. После того как обе диагонали будут проведены, соедините их концы, чтобы получить стороны квадрата. Поскольку для данного размера диагонали существует только одно возможное расположение сторон квадрата, квадрат, который мы построим, будет единственным возможным вариантом для таких диагоналей.
