
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Чему научились Глава 11 Дорофеев, Шарыгин — Подробные Ответы
Знаю соотношения между подмножествами множества рациональных чисел.
1. Верно ли утверждение:
а) всякое натуральное число является рациональным;
б) всякое рациональное число является целым;
в) всякое целое число является натуральным;
г) всякое натуральное число является целым?
Умею находить число, противоположное данному, применять знак «минус» для обозначения противоположного числа.
2. Назовите число, противоположное числу: 15,3; \(-\frac{1}{2}\); 0.
3. Пусть дано некоторое число \(a\). Как обозначить противоположное ему число? Чему равно \(-a\), если \(a=0,8\)? \(a=-15,2\)?
4. Запишите без скобок выражения \(+(+12)\), \(+(-10,5)\), \(-( +5,1)\), \(-\left(-\frac{1}{5}\right)\).
Умею отмечать на координатной прямой точки, соответствующие заданным числам, определять координаты отмеченных точек.
5. Отметьте на координатной прямой числа \(-6\); 2,5; \(-\frac{1}{2}\); \(3\frac{1}{2}\).
6. Запишите координаты точек, отмеченных на координатной прямой.
Знаю, что означает термин «модуль числа»; умею определять модуль числа.
7. Чему равен модуль числа: 2,8; -5,6; 0? Найдите \(|-27|\), \(|18|\), \(\left|-\frac{7}{8}\right|\), \(|4,1|\).
8. Отметьте на координатной прямой числа, модуль которых равен 4.
Умею сравнивать рациональные числа.
9. Сравните числа: а) 0 и -2,5; б) -3,4 и 1; в) \(-\frac{1}{2}\) и \(-\frac{3}{4}\).
Умею выполнять вычисления с рациональными числами, находить значения буквенных выражений, подставляя вместо букв заданные числа.
Вычислите (10-11).
10. а) \(-0,8 — 2,3\); б) \(-\frac{3}{4} + \frac{2}{3}\); в) \(\frac{1}{8} — \frac{5}{6}\); г) \(-2,5 + 7 — 1,5 — 10\).
11. а) \(-12 \cdot \frac{2}{3}\); б) \(8,1 : (-0,9)\); в) \(-\frac{2,4}{-0,6}\); г) \(-1,5 \cdot 3,4 \cdot (-10)\).
12. Найдите значение степени:
а) \(\left(-\frac{2}{3}\right)^2\);
б) \((-0,5)^3\).
13. Найдите значение выражения:
а) \(-1,2 \cdot (0,9 — 1,4)\);
б) \(\frac{-2,5 + 0,4}{-3}\).
14. Найдите значение выражения:
а) \(4a\), если \(a = -1,2\);
б) \(a — b\), если \(a = -\frac{1}{15}\), \(b = \frac{3}{5}\).
Умею определять координаты точки на координатной плоскости, строить точки с заданными координатами.
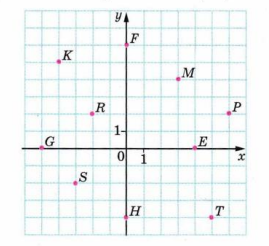
15. Запишите координаты точек, указанных на рисунке.
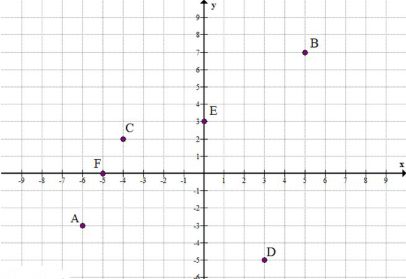
16. Постройте на координатной плоскости точки: \(A(-6; -3)\), \(B(5; 7)\), \(C(-4; 2)\), \(D(3; -5)\), \(E(0; 3)\), \(F(-5; 0)\).
1.
а) верно;
б) неверно, например, число 1,3 является рациональным, но не является целым;
в) неверно, например, число \(-7\) является целым, но не является натуральным;
г) верно.
2.
Числу 15,3 противоположно число \(-15,3\);
числу \(-\frac{1}{2}\) противоположно число \(\frac{1}{2}\);
числу 0 противоположно самому себе.
3.
Числу \(a\) противоположно число \(-a\).
Если \(a=0,8\), то \(-a=-0,8\);
если \(a=-15,2\), то \(-a=15,2\).
4.
\(+(+12)=12\);
\(+(-10,5)=-10,5\);
\(-( +5,1)=-5,1\);
\(-\left(-\frac{1}{5}\right)=\frac{1}{5}\).
5.
На координатной прямой отмечены числа: \(-6\), \(-\frac{1}{2}\), 0, 1, 2,5, \(3\frac{1}{2}\).
6.
а) координаты точек: \(-2\), 3, 5;
б) координаты точек: \(-5,2\), \(-5,5\), \(-5,7\).
7.
\(|2,8|=2,8\);
\(|-5,6|=5,6\);
\(|0|=0\);
\(|-27|=27\);
\(|18|=18\);
\(\left|-\frac{7}{8}\right|=\frac{7}{8}\);
\(|4,1|=4,1\).
8.
\(|x|=4 \implies x=\pm 4\).
9.
а) \(0 > -2,5\);
б) \(-3,4 < 1\);
в) \(-\frac{1}{2} > -\frac{3}{4}\) так как \(-\frac{2}{4} > -\frac{3}{4}\).
10.
а) \(-0,8 — 2,3 = -(0,8 + 2,3) = -3,1\);
б) \(-\frac{3}{4} + \frac{2}{3} = \frac{-9 + 8}{12} = -\frac{1}{12}\);
в) \(\frac{1}{8} — \frac{5}{6} = \frac{3 — 20}{24} = -\frac{17}{24}\);
г) \(-2,5 + 7 — 1,5 — 10 = -(2,5 + 1,5 + 10) + 7 = -14 + 7 = -7\).
11.
а) \(12 \cdot \frac{2}{3} = -4 \cdot 2 = -8\);
б) \(8,1 : (-0,9) = -81 : 9 = -9\);
в) \(-\frac{2,4}{-0,6} = \frac{24}{6} = 4\);
г) \(-1,5 \cdot 3,4 \cdot (-10) = 1,5 \cdot 10 \cdot 3,4 = 15 \cdot 3,4 = 51\).
12.
а) \(\left(-\frac{2}{3}\right)^2 = \frac{4}{9}\);
б) \((-0,5)^3 = -0,125\).
13.
а) \(-1,2 \cdot (0,9 — 1,4) = -1,2 \cdot (-0,5) = 0,6\);
б) \(\frac{-2,5 + 0,4}{-3} = \frac{-2,1}{-3} = 0,7\).
14.
а) при \(a = -1,2\), \(4a = 4 \cdot (-1,2) = -4,8\);
б) при \(a = -\frac{1}{15}\), \(b = \frac{3}{5}\),
\(a — b = -\frac{1}{15} — \frac{3}{5} = -\frac{1}{15} — \frac{9}{15} = -\frac{10}{15} = -\frac{2}{3}\).
15.
\(K(-4; 5)\); \(R(-2; 2)\); \(G(-5; 0)\); \(S(-3; -2)\); \(F(0; 6)\); \(H(0; -4)\); \(M(3; 4)\); \(P(6; 2)\); \(E(4; 0)\); \(T(5; -4)\).
16.
Построены точки:
\(A(-6; -3)\), \(B(5; 7)\), \(C(-4; 2)\), \(D(3; -5)\), \(E(0; 3)\), \(F(-5; 0)\).
№ 1.
а) Утверждение верно, потому что рациональные числа включают в себя все числа, которые можно представить в виде дроби \(\frac{m}{n}\), где \(m\) и \(n\) — целые числа, \(n \neq 0\). Целые числа — это частный случай рациональных, поэтому утверждение, что число является рациональным и целым, вполне корректно.
б) Утверждение неверно, примером служит число 1,3. Оно действительно рациональное, так как может быть записано в виде дроби \(\frac{13}{10}\), но при этом не является целым числом, так как целые числа — это числа без дробной части.
в) Утверждение неверно, так как число \(-7\) является целым числом, но не является натуральным. Натуральные числа — это положительные целые числа, начиная с 1, поэтому отрицательные целые числа к натуральным не относятся.
г) Утверждение верно, так как противоположное число для любого числа существует и определяется как число с тем же модулем, но противоположным знаком.
№ 2.
Число 15,3 противоположно числу \(-15,3\), так как противоположное число — это число, сумма которого с исходным равна нулю. То есть \(15,3 + (-15,3) = 0\).
Числу \(-\frac{1}{2}\) противоположно число \(\frac{1}{2}\), так как сумма этих чисел равна нулю: \(-\frac{1}{2} + \frac{1}{2} = 0\).
Числу 0 противоположно само число 0, поскольку \(0 + 0 = 0\), и оно является единственным числом, противоположным самому себе.
№ 3.
Числу \(a\) противоположно число \(-a\). Если \(a = 0,8\), то \(-a = -0,8\). Если \(a = -15,2\), то \(-a = 15,2\). Это объясняется определением противоположного числа: сумма числа и его противоположного равна нулю, то есть \(a + (-a) = 0\).
Противоположное число всегда меняет знак на противоположный, при этом абсолютное значение (модуль) остаётся неизменным.
Таким образом, для любого числа \(a\) существует единственное противоположное число \(-a\), и оно является отражением \(a\) относительно нуля на числовой оси.
№ 4.
Рассмотрим выражения:
\(+(+12) = 12\), так как знак «+» перед положительным числом не изменяет его значение.
\(+(-10,5) = -10,5\), знак «+» перед отрицательным числом сохраняет знак числа.
\(-( +5,1) = -5,1\), знак «-» меняет знак числа на противоположный.
\(-\left(-\frac{1}{5}\right) = \frac{1}{5}\), двойное отрицание меняет знак обратно на положительный.
№ 5.
На числовой оси показаны точки, соответствующие числам: \(-6\), \(-1\), \(0\), \(1\), \(2,5\), \(3\), \(3,1\), \(2\). Каждое число расположено в соответствии с его значением на оси \(x\).
Числовая ось помогает визуально определить порядок и расстояния между числами, а также понять расположение отрицательных и положительных значений относительно нуля.
Положительные числа расположены справа от нуля, отрицательные — слева, а ноль занимает центральное положение.
№ 6.
а) Множество чисел: \(-2\), \(3\), \(5\). Здесь представлены три целых числа, два из которых положительные и одно отрицательное.
б) Множество чисел: \(-5,2\), \(-5,5\), \(-5,7\). Все числа отрицательные и имеют дробную часть, что делает их рациональными, но не целыми.
Такие множества чисел позволяют классифицировать и упорядочивать числа по признакам знака и типа.
№ 7.
Модуль числа — это его абсолютное значение, то есть расстояние от нуля на числовой оси без учёта знака:
\(|2,8| = 2,8\);
\(|-5,6| = 5,6\);
\(|0| = 0\);
\(|-27| = 27\);
\(|18| = 18\);
\(\left|-\frac{7}{8}\right| = \frac{7}{8}\);
\(|4,1| = 4,1\).
Модуль всегда неотрицателен, он показывает величину числа без учёта его знака.
№ 8.
Если \(|x| = 4\), то \(x = \pm 4\), то есть \(x\) может быть либо \(4\), либо \(-4\).
Графически это отображается двумя точками на числовой оси: одна в точке \(4\), другая в точке \(-4\).
Это свойство модуля отражает симметрию относительно нуля на числовой оси.
№ 9.
а) Неравенство \(0 > -2,5\) верно, так как ноль больше любого отрицательного числа.
б) Неравенство \(-3,4 < 1\) верно, так как любое отрицательное число меньше положительного.
в) Неравенство \(-\frac{1}{2} > -\frac{3}{4}\) верно, так как \(-\frac{1}{2} = -0,5\) больше, чем \(-\frac{3}{4} = -0,75\).
Это объясняется тем, что на числовой оси число, расположенное правее, больше.
Таким образом, \(-\frac{2}{4} > -\frac{3}{4}\).
№ 10.
а) Выражение \(-0,8 — 2,3\) можно переписать как \(-(0,8 + 2,3) = -3,1\), то есть сумма чисел берётся в скобки с изменением знака.
б) Выражение \(-\frac{3}{4} + \frac{2}{3}\) приводится к общему знаменателю:
\(-\frac{3}{4} + \frac{2}{3} = \frac{-3 \cdot 3}{12} + \frac{2 \cdot 4}{12} = \frac{-9}{12} + \frac{8}{12} = -\frac{1}{12}\).
в) Выражение \(\frac{1}{8} — \frac{3}{6}\) также приводится к общему знаменателю:
\(\frac{1}{8} — \frac{3}{6} = \frac{3}{24} — \frac{12}{24} = -\frac{9}{24} = -\frac{3}{8}\).
г) Выражение \(-2,5 + 7 — 1,5 — 10\) можно сгруппировать:
\(- (2,5 + 1,5 + 10) + 7 = -14 + 7 = -7\).
№ 11.
а) Произведение \(-12 \cdot \frac{2}{3} = -4 \cdot 2 = -8\), так как \(-12 \cdot \frac{2}{3} = \frac{-12 \cdot 2}{3} = \frac{-24}{3} = -8\).
б) Деление \(8,1 : (-0,9) = -81 : 9 = -9\), так как \(8,1\) делится на \(-0,9\) с результатом \(-9\).
в) Выражение \(\frac{-2,4}{-0,6} = \frac{-24}{-6} = 4\), отрицательные знаки сокращаются.
г) Умножение \(-1,5 \cdot 3,4 \cdot (-10) = 1,5 \cdot 10 \cdot 3,4 = 15 \cdot 3,4 = 51\), знак меняется на положительный, так как произведение двух отрицательных чисел положительно.
№ 12.
а) Возведение в квадрат:
\(\left(-\frac{2}{3}\right)^2 = \left(-\frac{2}{3}\right) \cdot \left(-\frac{2}{3}\right) = \frac{2 \cdot 2}{3 \cdot 3} = \frac{4}{9}\).
б) Возведение в куб:
\((-0,5)^3 = (-0,5) \cdot (-0,5) \cdot (-0,5) = 0,25 \cdot (-0,5) = -0,125\).
Это показывает, что степень влияет на знак и величину числа: четная степень делает число положительным, а нечетная сохраняет знак исходного числа.
№ 13.
а) Вычисление произведения:
\(-1,2 \cdot (0,9 — 1,4) = -1,2 \cdot (-0,5) = 1,2 \cdot 0,5 = 0,6\).
б) Деление:
\(-2,5 + 0,4 = \frac{-2,1}{-3} = \frac{21}{30} = \frac{7}{10} = 0,7\).
Здесь показано, как преобразовываются выражения с отрицательными числами и дробями.
№ 14.
а) При \(a = -1,2\):
\(4a = 4 \cdot (-1,2) = -4,8\), умножение положительного числа на отрицательное даёт отрицательный результат.
б) При \(a = -\frac{1}{15}\), \(b = \frac{3}{5}\):
\(a — b = -\frac{1}{15} — \frac{3}{5} = -\frac{1}{15} — \frac{9}{15} = -\frac{10}{15} = -\frac{2}{3}\).
Здесь показано, как приводить дроби к общему знаменателю и выполнять вычитание.
№ 15.
Точки на координатной плоскости:
\(K(-4; 5)\), \(R(-2; 2)\), \(G(-5; 0)\), \(S(-3; -2)\), \(F(0; 6)\), \(H(0; -4)\), \(M(3; 4)\), \(P(6; 2)\), \(E(4; 0)\), \(T(5; -4)\).
Каждая точка задана парой координат \((x; y)\), где \(x\) — абсцисса, \(y\) — ордината.
Расположение точек на плоскости позволяет визуализировать их взаимное расположение и расстояния между ними.
№ 16.
Точки на координатной плоскости:
\(A(-6; -3)\), \(B(5; 7)\), \(C(-4; 2)\), \(D(3; -5)\), \(E(0; 3)\), \(F(-5; 0)\).
Координатная плоскость разбита на четыре квадранта, и каждая точка располагается в соответствии со знаками своих координат.



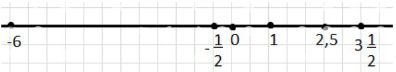



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!