Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Чему научились 5 Дорофеев, Шарыгин — Подробные Ответы
Чему вы научились
Обязательные умения
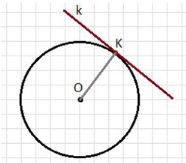
Умею строить касательную к окружности.
1. Начертите окружность, отметьте на ней какую-нибудь точку и постройте касательную к окружности в этой точке.
Знаю все случаи взаимного расположения двух окружностей на плоскости; умею определять взаимное расположение двух окружностей по заданным радиусам и расстоянию между их центрами.
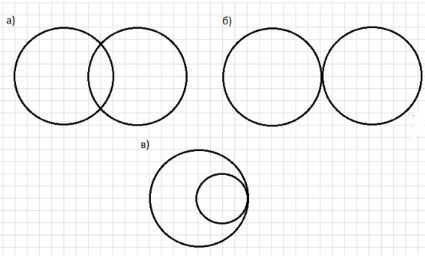
2. Изобразите следующие случаи взаимного расположения двух окружностей:
а) окружности пересекаются;
б) окружности касаются внешним образом;
в) окружности касаются внутренним образом.
3. Радиусы двух окружностей равны 7 см и 11 см, а расстояние между их центрами — 19 см. Как расположены по отношению друг к другу эти окружности?
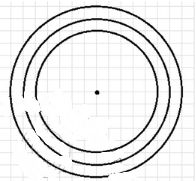
4. Начертите три концентрические окружности с радиусами 2,5 см, 3 см, 3,5 см.
Умею воспроизводить заданные изображения, составленные из окружностей, прямых и окружностей.
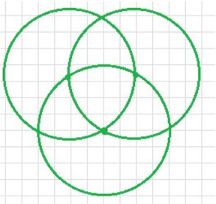
5. Воспроизведите рисунок, взяв радиус окружностей равным 2 см.
Умею строить треугольник по трём заданным сторонам.
6. Постройте:
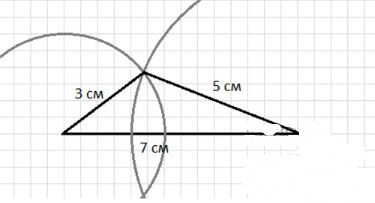
а) треугольник со сторонами, равными Зсм, 5 см и 7 см;
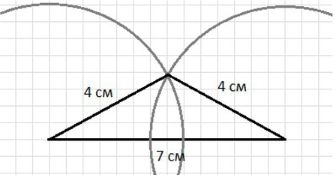
б) равнобедренный треугольник, основание которого равно 7 см, а боковые стороны — 4 см.
Различаю цилиндр, конус, шар; знаю, как в сечении поверхностей этих фигур плоскостью можно получить окружность, эллипс.
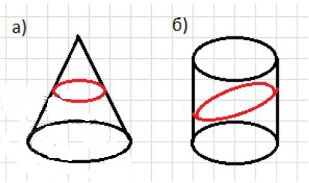
7. а) Скопируйте конус и нанесите на его изображение какое-нибудь сечение, имеющее форму окружности.
б) Скопируйте цилиндр и нанесите на его изображение какое-нибудь сечение, имеющее форму эллипса.
Чему вы научились
Обязательные умения:
1. Умею строить касательную к окружности.
— Начертите окружность, отметьте на ней точку и постройте касательную к окружности в этой точке.
2. Знаю все случаи взаимного расположения двух окружностей на плоскости и умею определять их по заданным радиусам и расстоянию между центрами.
- а) Окружности пересекаются, если расстояние между центрами меньше суммы радиусов, но больше разности радиусов.
- б) Окружности касаются внешним образом, если расстояние между центрами равно сумме радиусов.
- в) Окружности касаются внутренним образом, если расстояние между центрами равно разности радиусов.
3. Даны радиусы 7 см и 11 см, расстояние между центрами 19 см.
Сумма радиусов: 7 + 11 = 18 см.
Разность радиусов: 11 — 7 = 4 см.
Поскольку расстояние между центрами (19 см) больше суммы радиусов (18 см), окружности не пересекаются и не касаются — они находятся отдельно друг от друга.
4. Начертите три концентрические окружности с радиусами 2,5 см, 3 см и 3,5 см. Центры окружностей совпадают.
5. Воспроизведите рисунок, используя окружности радиусом 2 см.
6. Постройте треугольники:
- а) со сторонами 3 см, 5 см и 7 см;
- б) равнобедренный треугольник с основанием 7 см и боковыми сторонами 4 см.
7. Различаю цилиндр, конус и шар, знаю, какие сечения дают окружность и эллипс.
- а) Скопируйте конус и нанесите сечение в форме окружности (плоскость, параллельная основанию конуса).
- б) Скопируйте цилиндр и нанесите сечение в форме эллипса (плоскость, наклонённая к основанию цилиндра).
Чему вы научились
Обязательные умения и навыки:
1. Умею строить касательную к окружности.
Для этого нужно начертить окружность, выбрать на ней любую точку и провести прямую, касающуюся окружности именно в этой точке. Касательная будет перпендикулярна радиусу, проведённому в точку касания.
2. Знаю все случаи взаимного расположения двух окружностей на плоскости и умею определять их положение по заданным радиусам и расстоянию между центрами окружностей.
- а) Окружности пересекаются, если расстояние между центрами меньше суммы радиусов, но больше их разности.
- б) Окружности касаются внешним образом, если расстояние между центрами равно сумме радиусов.
- в) Окружности касаются внутренним образом, если расстояние между центрами равно разности радиусов.
3. Даны две окружности с радиусами 7 см и 11 см, расстояние между центрами которых равно 19 см.
Сумма радиусов: 7 + 11 = 18 см.
Разность радиусов: 11 — 7 = 4 см.
Поскольку расстояние между центрами (19 см) больше суммы радиусов (18 см), окружности не касаются и не пересекаются, они расположены отдельно друг от друга.
4. Умею начертить три концентрические окружности, то есть окружности с одним центром, но разными радиусами — 2,5 см, 3 см и 3,5 см.
Это упражнение помогает понять понятие концентричности и визуализировать разницу в радиусах.
5. Умею воспроизводить заданные изображения, составленные из окружностей и прямых линий.
Например, можно воспроизвести рисунок, используя окружности с радиусом 2 см, повторяя и комбинируя элементы рисунка.
6. Умею строить треугольник по трём заданным сторонам.
- а) Построить треугольник со сторонами 3 см, 5 см и 7 см, используя линейку и циркуль.
- б) Построить равнобедренный треугольник, в котором основание равно 7 см, а боковые стороны — по 4 см.
7. Различаю основные геометрические тела: цилиндр, конус и шар.
Знаю, что в сечениях этих фигур плоскостью можно получить разные формы:
- а) На изображении конуса можно провести сечение, которое будет иметь форму окружности — например, если плоскость параллельна основанию конуса.
- б) На изображении цилиндра можно провести сечение в виде эллипса — если плоскость сечения наклонена относительно основания цилиндра.
Эти умения помогают лучше понимать свойства фигур и развивают пространственное мышление.
