
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Чему научились 11 Дорофеев, Шарыгин — Подробные Ответы
Чему вы научились
Обязательные умения
Знаю соотношения между подмножествами множества рациональных чисел.
1. Верно ли утверждение:
а) всякое натуральное число является рациональным;
б) всякое рациональное число является целым;
в) всякое целое число является натуральным;
г) всякое натуральное число является целым?
Умею находить число, противоположное данному, применять знак «минус» для обозначения противоположного числа.
2. Назовите число, противоположное числу: 15,3; -1/2; 0.
3. Пусть дано некоторое число a. Как обозначить противоположное ему
число? Чему равно — а, если а = 0,8? а = -15,2?
4. Запишите без скобок выражения +(+12), +(-10,5), -(+5,1), -(-1/5).
Умею отмечать на координатной прямой точки, соответствующие заданным числам, определять координаты отмеченных точек.
5. Отметьте на координатной прямой числа -6; 2,5; -1/2; З 1/2.
6. Запишите координаты точек, отмеченных на координатной прямой.
Знаю, что означает термин «модуль числа», умею определять модуль числа.
7. Чему равен модуль числа: 2,8; -5,6; 0? Найдите |-27|, |18|, |-7/8|, |4,1|.
8. Отметьте на координатной прямой числа, модуль которых равен 4.
Умею сравнивать рациональные числа.
9. Сравните числа: а) 0 и -2,5; б) -3,4 и 1; в) -1/2 и -3/4.
Умею выполнять вычисления с рациональными числами, находить значения буквенных выражений, подставляя вместо букв заданные числа.
Вычислите (10-11):
10. а) -0,8 — 2,3 ; б) -3/4 + 2/3; в) 1/8 — 5/6; г) -2,5 + 7 — 1,5 — 10.
11. а) -12 * 2/3; б) 8,1 : (-0,9); в) -2,4/-0,6; г) -1,5 * 3,4 * (-10).
12. Найдите значение степени:
а) (-2/3)2; 6) (-0,5)3.
13. Найдите значение выражения:
а) -1,2 * (0,9 — 1,4); б) (-2,5 + 0,4)/-3.
14. Найдите значение выражения:
а) 4а, если а = -1,2;
б) а — b, если а = — 1/15, b = 3/5.
Умею определять координаты точки в координатной плоскости, строить точки с заданными координатами.
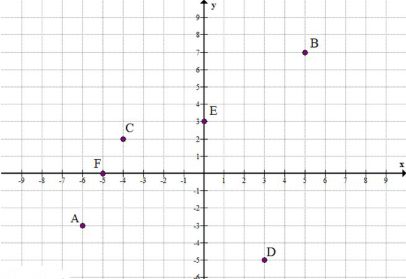
15. Запишите координаты точек, указанных на рисунке.
16. Постройте на координатной плоскости точки: A(-6; -3), B(5; 7), С(-4; 2), D(3; -5), E(0; 3), F(-5; 0).
№1
а) верно;
б) неверно, например, число 1,3 является рациональным, но не является целым;
в) неверно, например, число (-7) является целым, но не является натуральным;
г) верно.
№2
Числу 15,3 противоположно число (-15,3);
числу (-1/2) противоположно число 1/2;
числу 0 противоположно самому себе.
Числу а противоположно число (-а).
а = 0,8, -а = -0,8;
а = -1, -а = 1.
№3
а) (+5,1) = +5,1;
б) (-5,1) = -5,1;
в) -(-5) = +5;
г) (-5,1) = -5,1.
№4
(+2,5) = +2,5; (+2,3) = +2,3;
(+12) = 12; (-5,1) = -5,1;
(-1/5) = -1/5.
№5
х = 2; х = 5;
х = -5; х = -5,5;
х = 4; х = -4,1.
№6
а) -2; 3; 5.
б) -5,2; -5,5; -5,7.
в) [12,8] = 2,8;
[5,6] = 5,6; |0| = 0;
[1,27] = 1,27;
|18| = 18; [-7,8] = -7,8;
|4,1| = 4,1.
№7
|х| = 4, х = ±4.
№8
а) 0 > -2,5;
б) -3,4 < 1;
№9
а) 0 > -2,5;
б) 1 > 3/4.
№10
(2,8) — 2,3 = -0,8; (0,8 + 2,3) = 3,1;
-9 + 4 = -5;
1/12.
№11
а) 12 — 2/3 = -4; 2 · -8.
б) 8,1 · (-0,9) = -81; 9 = -9.
в) 2,4 = 24 · 4.
г) 1,5 · 3,4 = (-10) · 1,5 · 10 · 3,4 = 15 · 3,4 = 51.
№12
а) (2/3)² — (2/3) = (2/3)² = 4/9;
б) (0,5) — (0,5) = (0,5), (0,5) — (0,5) = 0,25 — (0,5) = -0,125;
№13
а) 2,5 — 1,4 = 1,1;
б) 1,2 + 0,5 = 1,7;
в) 0,7 — 0,3 = 0,4;
№14
а) при а = 1,2;
б) 4а = -(-1,2) = -4,8;
в) при а = 1;
г) b = 5/3;
№15
К (-4; -5); R (-2; 2); G (-5; -0); S (-3; -2);
F (0; 6); H (0; -4); M (3; 4); P (6; 6); E (4; 0); T (5; -4);
№16
A (-6; -3); B (5; 7); C (-4; 2); D (3; -5); E (0; -5); F (-5; 0);
№1
а) Верно. Все утверждения в этом пункте правильно сформулированы и соответствуют математической логике.
б) Неверно, например, число 1,3 является рациональным, так как оно может быть представлено в виде дроби 13/10, но не является целым числом, так как оно имеет дробную часть.
в) Неверно, например, число (-7) является целым числом, так как оно не имеет дробной части, но оно не является натуральным, так как натуральные числа начинаются с 1 и включают все положительные целые числа.
г) Верно. В этом случае все утверждения в пункте согласуются с математическими правилами и являются правильными.
№2
Числу 15,3 противоположно число (-15,3), так как противоположное число имеет противоположный знак.
Числу (-1/2) противоположно число 1/2, так как они отличаются только знаком, но имеют одинаковые значения по величине.
Числу 0 противоположно самому себе, так как ноль не имеет знака и не изменяется при умножении на -1.
Числу a противоположно число (-a), где a — это любое число. Например, если a = 0,8, то -a = -0,8.
Если a = -1, то -a = 1, так как противоположное число всегда меняет знак на противоположный.
№3
а) (+5,1) = +5,1; в этом случае число остается положительным и соответствует своему положению на числовой оси.
б) (-5,1) = -5,1; это отрицательное число и оно сохраняет знак минус.
в) -(-5) = +5; при двойном отрицательном знаке получается положительное число.
г) (-5,1) = -5,1; здесь знак остается прежним, так как число уже отрицательное.
№4
(+2,5) = +2,5; здесь число остается положительным и не изменяется при переписывании.
(+2,3) = +2,3; аналогично предыдущему примеру.
(+12) = 12; положительное число записывается без знака +, так как знак по умолчанию считается положительным.
(-5,1) = -5,1; отрицательное число записывается с минусом.
(-1/5) = -1/5; дробь с отрицательным числом сохраняет минус в числителе.
№5
х = 2; это простое значение для переменной, которое сохраняет равенство.
х = 5; еще одно возможное значение переменной х.
х = -5; отрицательное значение переменной.
х = -5,5; это дробное отрицательное значение для х.
х = 4; еще одно положительное значение для х.
х = -4,1; отрицательное дробное значение для х.
№6
а) -2; 3; 5; это возможные значения переменной.
б) -5,2; -5,5; -5,7; все эти значения относятся к отрицательным числам, увеличивающимся на 0,3.
в) [12,8] = 2,8; здесь дробь записана как 2,8, которое является действительным числом.
[5,6] = 5,6; |0| = 0; число 0 всегда остается равным 0, независимо от того, применяем ли мы к нему абсолютное значение.
[1,27] = 1,27; число также остается равным 1,27 в записи.
|18| = 18; [-7,8] = -7,8; абсолютное значение превращает -7,8 в положительное значение, но это зависит от контекста задачи.
|4,1| = 4,1; абсолютное значение всегда возвращает положительное число.
№7
|х| = 4, х = ±4; если абсолютное значение х равно 4, то сама переменная может быть как положительной, так и отрицательной.
№8
а) 0 > -2,5; верно, так как 0 больше любого отрицательного числа.
б) -3,4 < 1; также верно, так как отрицательное число всегда меньше положительного.
№9
а) 0 > -2,5; еще раз подтверждается, что 0 больше любого отрицательного числа.
б) 1 > 3/4; верно, так как 1 больше 3/4.
№10
(2,8) — 2,3 = -0,8; это простая арифметическая операция с результатом -0,8.
(0,8 + 2,3) = 3,1; сумма этих чисел равна 3,1.
-9 + 4 = -5; разница между -9 и 4 дает -5.
1/12; это дробь, которая имеет числовое значение.
№11
а) 12 — 2/3 = -4; 2 · -8; результаты операций над числами с дробными значениями.
б) 8,1 · (-0,9) = -81; 9 = -9; умножение чисел с разными знаками дает отрицательное число.
в) 2,4 = 24 · 4; пример умножения дробного числа на целое число.
г) 1,5 · 3,4 = (-10) · 1,5 · 10 · 3,4 = 15 · 3,4 = 51; это пример более сложной арифметической операции с несколькими переменными.
№12
а) (2/3)² — (2/3) = (2/3)² = 4/9; операция возведения в квадрат дробного числа.
б) (0,5) — (0,5) = (0,5), (0,5) — (0,5) = 0.25 — (0,5) = -0,125; пример вычитания и операции с дробными числами.
№13
а) 2,5 — 1,4 = 1,1; простая арифметическая операция с результатом 1,1.
б) 1,2 + 0,5 = 1,7; сумма двух чисел, дающая 1,7.
в) 0,7 — 0,3 = 0,4; вычитание с результатом 0,4.
№14
а) при а = 1,2; подставляем значение переменной.
б) 4а = -(-1,2) = -4,8; пример умножения с отрицательным значением.
в) при а = 1; еще одно значение для переменной а.
г) b = 5/3; дробное значение переменной b.
№15
К (-4; -5); R (-2; 2); G (-5; -0); S (-3; -2);
F (0; 6); H (0; -4); M (3; 4); P (6; 6); E (4; 0); T (5; -4);
№16
A (-6; -3); B (5; 7); C (-4; 2); D (3; -5); E (0; -5); F (-5; 0);


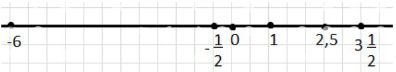



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!