Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 994 Дорофеев, Шарыгин, Суворова — Подробные Ответы
Экспериментируем.
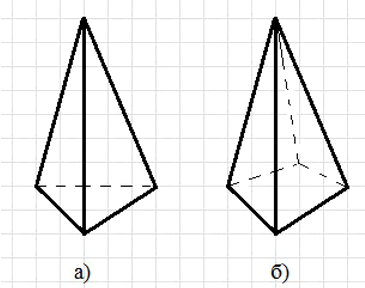
1) Скопируйте рисунок 10.50 в тетрадь и дорисуйте его до: а) треугольной пирамиды; б) четырёхугольной пирамиды.
2) Представьте, что у многогранника, изображённого на рисунке 10.50, пять вершин, но одна вершина не нарисована. Как вы думаете, сколько можно придумать многогранников с пятью вершинами, чтобы у них было разное число рёбер?
- Дорисовка:
а) Для треугольной пирамиды основание — треугольник, вершина соединяется с его вершинами.
б) Для четырёхугольной пирамиды основание — четырёхугольник, вершина соединяется с его вершинами. - У многогранника с пятью вершинами всегда восемь рёбер. Невозможно придумать многогранники с пятью вершинами и разным числом рёбер.
1) Дорисовка рисунка 10.50 до пирамид:
На рисунке 10.50 изображён многогранник, который можно дополнить до пирамид. Рассмотрим два варианта:
а) Треугольная пирамида:
Для того чтобы получить треугольную пирамиду, нужно выбрать треугольник в основании (любой из треугольников, образованных рёбрами многогранника) и соединить его вершины с одной общей точкой, которая будет вершиной пирамиды. Например, если основанием выбрать треугольник, образованный нижней гранью, то вершина пирамиды будет соединена с каждой из трёх вершин основания.
б) Четырёхугольная пирамида:
Для получения четырёхугольной пирамиды нужно выбрать основание в виде четырёхугольника. Например, если основанием выбрать нижнюю грань, которая является четырёхугольником, то оставшуюся вершину соединяем с каждой из вершин основания. Таким образом, получается четырёхугольная пирамида.
2) Сколько можно придумать многогранников с пятью вершинами, чтобы у них было разное число рёбер?
У многогранника с пятью вершинами всегда будет восемь рёбер. Это связано с тем, что число рёбер определяется количеством граней и связями между вершинами. В данном случае, если у многогранника пять вершин, то он всегда будет иметь фиксированное число рёбер.
Объяснение:
Для многогранника с пятью вершинами минимально возможное число рёбер — 8. Это можно проверить по формуле Эйлера для многогранников:
V — E + F = 2,
где V — количество вершин, E — количество рёбер, F — количество граней.
Подставляя V = 5 и решая уравнение, получаем, что E фиксировано и равно 8.
Ответ: Придумать многогранники с пятью вершинами, чтобы у них было разное число рёбер, невозможно.
Математика
