ГДЗ по Математике 5 Класс Номер 956 Дорофеев, Шарыгин, Суворова — Подробные Ответы

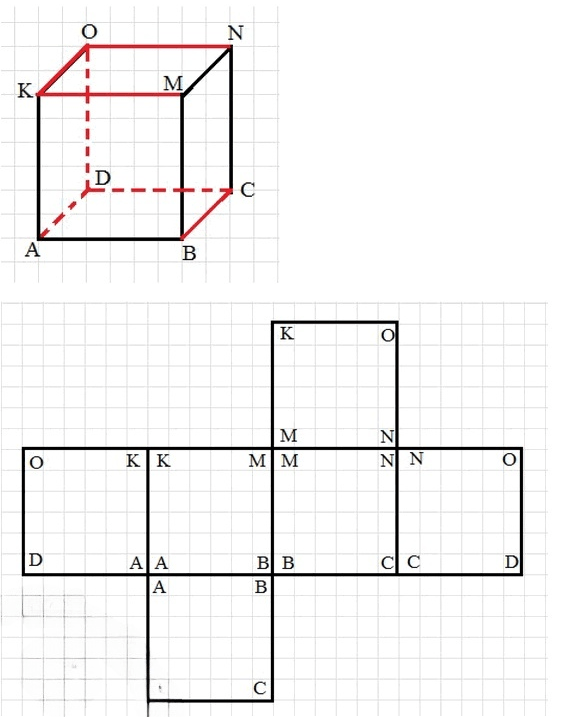
По каким рёбрам можно разрезать куб (рис. 10.29), чтобы получить развёртку под номером 3 (см. рис. 10.16)? Нарисуйте куб в тетради и покажите какую-нибудь линию разреза.

Подсказка. Воспользуйтесь моделью куба.

На рисунке представлен куб, который нужно разрезать таким образом, чтобы получилась развёртка под номером 3 (см. рис. 10.16). Рассмотрим, какие рёбра нужно разрезать для получения такой развёртки.

Анализируем развёртку под номером 3.

Развёртка состоит из одной центральной грани, к которой примыкают 4 боковые грани (сверху, снизу, справа и слева) и одна грань, расположенная снизу от центральной.

Это характерная форма креста, где центральная грань соединяет все остальные.

Определяем линии разрезов.

Центральной гранью в кубе выберем грань КМНО.

К этой грани примыкают:

Грань ABCD снизу;

Грань КАОD слева;

Грань МBNC справа;

Грань КМAB сверху.

Чтобы получить требуемую развёртку, нужно выполнить разрезы по следующим рёбрам:

KM, чтобы отделить верхнюю грань;

KO, чтобы отделить левую грань;

ON, чтобы отделить правую грань;

OD, чтобы отделить нижнюю грань.

Проверяем развёртку.

После выполнения указанных разрезов развёртка будет соответствовать форме креста, где центральная грань соединяет все остальные.

Вывод:
Для получения развёртки под номером 3 нужно разрезать куб по рёбрам: KM, KO, ON, OD.