Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 941 Дорофеев, Шарыгин, Суворова — Подробные Ответы
Наблюдаем и рассуждаем. На рисунке 10.20 изображён параллелепипед. Известны длины его рёбер: АВ = 6 см, ML = 4 см, АМ = 2 см.
1) Определите длины всех рёбер данного параллелепипеда.
2) Каковы размеры граней AMNB, BNKC, MLKN? Для каждой из них назовите равные ей грани.
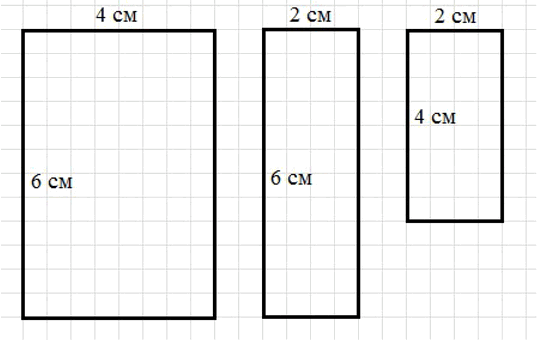
3) Начертите три различные грани параллелепипеда в натуральную величину.
4) Найдите сумму площадей всех граней параллелепипеда.
Длины рёбер:
AM = DL = CK = BN = 2 см;
ML = NK = BC = AD = 4 см;
AB = MN = LK = DC = 6 см.
Размеры граней:
Грани AMNB и DLKC имеют ширину 2 см и длину 6 см.
Грани BNKC и AMLD имеют ширину 2 см и длину 4 см.
Грани MLKN и ADCB имеют ширину 4 см и длину 6 см.
Три различные грани параллелепипеда:
4 см × 6 см,
2 см × 6 см,
2 см × 4 см.
Площади граней:
Площадь граней AMNB и DLKC:
S1 = 2 × 6 × 2 = 24 см².
Площадь граней BNKC и AMLD:
S2 = 2 × 4 × 2 = 16 см².
Площадь граней MLKN и ADCB:
S3 = 4 × 6 × 2 = 48 см².
Сумма площадей всех граней параллелепипеда:
S = S1 + S2 + S3 = 24 + 16 + 48 = 88 см².
Ответ: 88 см².
Дано: параллелепипед, у которого размеры рёбер следующие:
AM = DL = CK = BN = 2 см (высота),
ML = NK = BC = AD = 4 см (ширина),
AB = MN = LK = DC = 6 см (длина).
Шаг 1. Определяем размеры граней параллелепипеда.
Параллелепипед имеет 6 граней, которые можно сгруппировать в три пары одинаковых прямоугольников:
- Грани AMNB и DLKC имеют размеры 2 см × 6 см (ширина × длина).
- Грани BNKC и AMLD имеют размеры 2 см × 4 см (высота × ширина).
- Грани MLKN и ADCB имеют размеры 4 см × 6 см (ширина × длина).
Шаг 2. Вычисляем площадь каждой пары граней.
Площадь каждой пары граней вычисляется как удвоенная площадь одной грани.
- Для граней AMNB и DLKC:
Площадь одной грани = 2 см × 6 см = 12 см².
Площадь двух таких граней = 12 см² × 2 = 24 см². - Для граней BNKC и AMLD:
Площадь одной грани = 2 см × 4 см = 8 см².
Площадь двух таких граней = 8 см² × 2 = 16 см². - Для граней MLKN и ADCB:
Площадь одной грани = 4 см × 6 см = 24 см².
Площадь двух таких граней = 24 см² × 2 = 48 см².
Шаг 3. Находим сумму площадей всех граней.
Сумма площадей всех граней параллелепипеда:
24 см² (AMNB и DLKC) + 16 см² (BNKC и AMLD) + 48 см² (MLKN и ADCB) = 88 см².
Ответ: площадь поверхности параллелепипеда равна 88 см².
Математика
