ГДЗ по Математике 5 Класс Номер 939 Дорофеев, Шарыгин, Суворова — Подробные Ответы

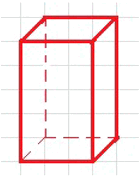
Скопируйте изображение параллелепипеда (рис. 10.18) в тетрадь и дорисуйте невидимые рёбра штриховой линией.

Для выполнения задания необходимо дорисовать невидимые рёбра параллелепипеда на рисунке (рис. 10.18). Рассмотрим процесс подробно.

1. Анализ видимых рёбер
На рисунке изображён параллелепипед с 8 вершинами и 12 рёбрами. Видимые рёбра обозначены сплошными линиями. Они показывают передние и верхние грани параллелепипеда, которые находятся ближе к наблюдателю.

2. Невидимые рёбра
Невидимые рёбра – это те, которые находятся за передними гранями параллелепипеда. Они представляют собой:

2 рёбра задней вертикальной грани, параллельные передним вертикальным рёбрам.

2 рёбра задней горизонтальной грани, параллельные нижнему и верхнему горизонтальным рёбрам.

2 рёбра, соединяющие заднюю грань с передней (диагональные рёбра, уходящие в глубину).

3. Как дорисовать невидимые рёбра

Используем штриховую линию для обозначения невидимых рёбер.

Рисуем рёбра, параллельные уже существующим на переднем плане:

Задние вертикальные рёбра параллельны передним вертикальным.

Задние горизонтальные рёбра параллельны передним горизонтальным.

Соединяющие рёбра параллельны диагоналям верхней и нижней граней.

4. Проверка правильности
После дорисовки рёбер убедитесь, что:

У параллелепипеда 12 рёбер.

Все рёбра соединяют вершины, и каждая вершина имеет 3 рёбра.

Штриховые линии чётко показывают задние грани и глубину фигуры.

Вывод
Невидимые рёбра параллелепипеда дорисовываются с использованием штриховой линии. В результате параллелепипед становится трёхмерным и визуально понятным.