ГДЗ по Математике 5 Класс Номер 934 Дорофеев, Шарыгин, Суворова — Подробные Ответы

Задача

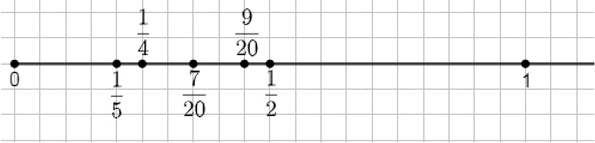
Назовите какие-нибудь три дроби, заключённые между числами 1/5 и 1/2. Изобразите все пять дробей точками на координатной прямой, выбрав подходящий единичный отрезок.

Краткий ответ:

1/5 = 4/20; 1/2 = 10/20.

Значит, между числами 1/5 и 1/2 заключены дроби:

5/20 = 1/4; 7/20; 9/20.

Единичный отрезок равен 20 клеткам.

Подробный ответ:

Приведение дробей к общему знаменателю
Чтобы сравнить дроби 1/5 и 1/2, приведём их к общему знаменателю. Наименьший общий знаменатель (НОЗ) для 5 и 2 равен 20.

Преобразуем 1/5:
1/5 = 4/20 (умножаем числитель и знаменатель на 4).
Преобразуем 1/2:
1/2 = 10/20 (умножаем числитель и знаменатель на 10).

Таким образом, дроби 1/5 и 1/2 равны 4/20 и 10/20 соответственно.

Поиск дробей между 1/5 и 1/2
Между дробями 4/20 и 10/20 находятся дроби, у которых числитель больше 4, но меньше 10, а знаменатель равен 20.
Выберем три таких дроби:

5/20 (эта дробь равна 1/4);
7/20;
9/20.

Построение координатной прямой
На координатной прямой единичный отрезок равен 20 клеткам. Это означает, что каждая клетка соответствует дроби с знаменателем 20.
Отметим на прямой следующие точки:

4/20 (это 1/5);

5/20 (это 1/4);

7/20;

9/20;

10/20 (это 1/2).

Оцени решение