ГДЗ по Математике 5 Класс Номер 930 Дорофеев, Шарыгин, Суворова — Подробные Ответы

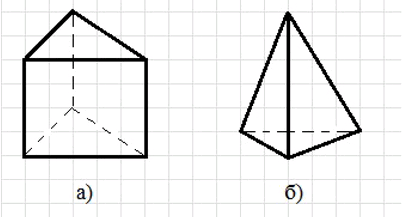
Перерисуйте многогранники, изображённые на рисунке 10.8, так, чтобы видимые грани стали невидимыми, а невидимые — видимыми.

Анализ задачи:
На рисунке 10.8 изображены два многогранника:

• а) усечённый куб, у которого верхняя часть меньше нижней, что создаёт наклонные боковые грани.
• б) пирамида с квадратным основанием, у которой видны три боковые грани, а четвёртая грань (задняя) невидима.

Необходимо перерисовать эти многогранники так, чтобы видимые грани стали невидимыми, а невидимые — видимыми.

Решение для фигуры а):

У фигуры а) видны три боковые грани, верхняя грань и часть нижней грани.

Если сделать видимые грани невидимыми, то:

Верхняя грань станет невидимой.

Части нижней грани, которые видны, тоже станут невидимыми.

Задние боковые грани, которые сейчас невидимы, станут видимыми.

Для изображения:

Линии, которые сейчас сплошные, нужно заменить на пунктирные (для невидимых частей).

Линии, которые сейчас пунктирные, нужно сделать сплошными.

Решение для фигуры б):

У фигуры б) видны три боковые грани, а задняя грань невидима.

Если сделать видимые грани невидимыми, то:

Левая, правая и передняя грани пирамиды станут невидимыми.

Задняя грань, которая сейчас невидима, станет видимой.

Для изображения:

Линии передних рёбер пирамиды нужно заменить на пунктирные.

Линии заднего ребра и задней грани сделать сплошными.

Вывод:
После перерисовки фигуры будут выглядеть так, что текущие видимые грани станут невидимыми, а текущие невидимые грани — видимыми.