ГДЗ по Математике 5 Класс Номер 929 Дорофеев, Шарыгин, Суворова — Подробные Ответы

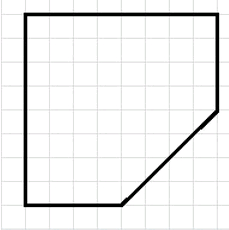
Наблюдаем и рассуждаем. От куба отрезали угол (рис. 10.10).
1) Сколько граней у получившегося многогранника? Какую форму они имеют? Сколько у него вершин? Сколько рёбер? Сколько граней на этом рисунке не видно? А вершин?
2) Как вы думаете, сколько граней будет у этого многогранника, если отрезать ещё один угол?
3) Начертите пятиугольную грань, если известно, что ребро куба равно 4 см, а разрез проходит через середины рёбер куба.

1. У получившегося многогранника 7 граней.
   3 грани в форме квадрата; 3 грани в форме пятиугольника; 1 грань в форме треугольника.
   Вершин — 10. Ребер — 15. Не видно — 3 грани и 1 вершину.
2. Если у этого многогранника отрезать еще один угол, то у него будет 8 граней.
3. Пятиугольная грань:

Анализ задачи:
У нас есть многогранник с 7 гранями:

3 грани в форме квадрата,

3 грани в форме пятиугольника,

1 грань в форме треугольника.

Также известно, что у многогранника 10 вершин и 15 рёбер. Не видно 3 грани и 1 вершину.

Проверка формулы Эйлера для многогранников:
Формула Эйлера для выпуклых многогранников:
вершины + грани — рёбра = 2.
Подставляем данные:
10 + 7 — 15 = 2.
Равенство выполняется, значит, многогранник корректен.

Увеличение количества граней:
Если отрезать ещё один угол, то у многогранника добавится одна новая грань.
Таким образом, количество граней увеличится с 7 до 8.

Ответ:
После отрезания угла у многогранника будет 8 граней.