ГДЗ по Математике 5 Класс Номер 919 Дорофеев, Шарыгин, Суворова — Подробные Ответы
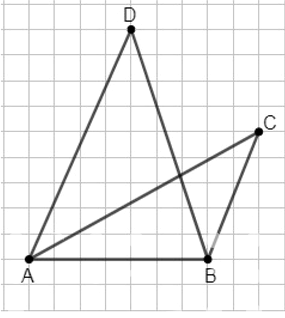
Выполните в тетради следующие построения: отметьте в узле сетки точку А; отступите на 7 клеток вправо и отметьте точку В; от точки В отступите на 2 клетки вправо и на 5 клеток вверх, отметьте точку С; от точки С отступите на 5 клеток влево и на 4 клетки вверх, отметьте точку D. Постройте треугольники АВС и АBD. Выполните необходимые измерения и определите, у какого из этих треугольников периметр больше.
- Периметр треугольника ABC:
Pₐ∆ABC = 3 см 5 мм + 2 см 7 мм + 5 см 2 мм = 11 см 4 мм. - Периметр треугольника ABD:
Pₐ∆ABD = 3 см 5 мм + 5 см + 4 см 8 мм = 13 см 3 мм. - Сравнение:
13 см 3 мм > 11 см 4 мм.
Ответ: периметр треугольника ABD больше.
Даны стороны треугольников:
AB = 3 см 5 мм, BC = 2 см 7 мм, AC = 5 см 2 мм, AD = 5 см, BD = 4 см 8 мм.
1. Найдём периметр треугольника ABC:
Периметр треугольника вычисляется как сумма длин его сторон:
Pₐ∆ABC = AB + BC + AC.
Подставим значения:
Pₐ∆ABC = 3 см 5 мм + 2 см 7 мм + 5 см 2 мм.
Сложим отдельно сантиметры и миллиметры:
- Сантиметры: 3 + 2 + 5 = 10 см.
- Миллиметры: 5 + 7 + 2 = 14 мм.
Так как 14 мм = 1 см 4 мм, добавим это к сантиметрам:
10 см + 1 см 4 мм = 11 см 4 мм.
Итак, периметр треугольника ABC равен 11 см 4 мм.
2. Найдём периметр треугольника ABD:
Периметр треугольника ABD вычисляется как сумма длин его сторон:
Pₐ∆ABD = AB + AD + BD.
Подставим значения:
Pₐ∆ABD = 3 см 5 мм + 5 см + 4 см 8 мм.
Сложим отдельно сантиметры и миллиметры:
- Сантиметры: 3 + 5 + 4 = 12 см.
- Миллиметры: 5 + 8 = 13 мм.
Так как 13 мм = 1 см 3 мм, добавим это к сантиметрам:
12 см + 1 см 3 мм = 13 см 3 мм.
Итак, периметр треугольника ABD равен 13 см 3 мм.
3. Сравним периметры:
Периметр треугольника ABD (13 см 3 мм) больше периметра треугольника ABC (11 см 4 мм).
Ответ: периметр треугольника ABD больше.
