ГДЗ по Математике 5 Класс Номер 901 Дорофеев, Шарыгин, Суворова — Подробные Ответы

Задача

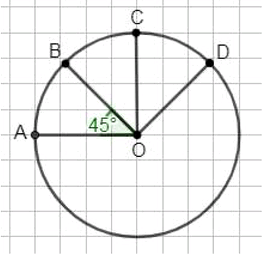
Постройте в тетради отрезок ОА и проведите окружность радиусом ОА. Проведите радиусы ОВ, ОС и ОD так, чтобы ∠АОВ = 45°, ∠АОС = 90°, ∠АОD = 135° (транспортир не используйте). Чему равен угол DОВ?

Краткий ответ:

45° — это половина 90°.
135° — это три раза по 45°.

∠DOB = два раза по 45° = 45 · 2 = 90°.
Ответ: ∠DOB = 90°.

Подробный ответ:

Дано окружность с центром в точке O. Угол AOC равен 45°. Нужно найти угол DOB, который является центральным углом.

Определим угол AOC.
По условию, угол AOC равен 45°. Это половина прямого угла, так как 90° ÷ 2 = 45°.
Рассмотрим угол AOD.
Угол AOD состоит из двух углов: AOC и COD. Нам известно, что угол COD равен трём углам AOC, то есть 45° × 3 = 135°.
Найдём угол DOB.
Угол DOB равен удвоенному углу AOC, так как он охватывает два одинаковых угла AOC. Таким образом:
угол DOB = 45° × 2 = 90°.

Ответ: угол DOB = 90°.

Краткое решение

Угол AOC = 45°. Угол COD = 135°. Угол DOB = 45° × 2 = 90°.
Ответ: угол DOB = 90°.

Оцени решение