Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 822 Дорофеев, Шарыгин, Суворова — Подробные Ответы
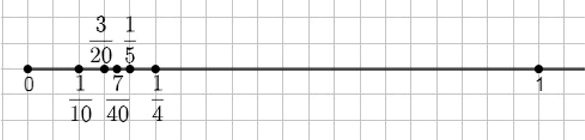
Изобразите на координатной прямой дроби 1/10 и 1/4 (возьмите в качестве единичного отрезка 20 клеток тетради). Назовите три дроби, заключённые между числами 1/10 и 1/4, и изобразите их точками на координатной прямой.
Единичный отрезок равен 20 клеткам.
1/10 = 2/20;
1/4 = 5/20.
На координатной прямой:
- 3/20,
- 7/40,
- 1/5 заключены между числами 1/10 и 1/4.
1. Изобразим дроби 1/10 и 1/4 на координатной прямой.
Единичный отрезок:
По условию задачи, единичный отрезок равен 20 клеткам тетради. Это значит, что 1 клетка соответствует 1/20.
Рассчитаем положение дробей 1/10 и 1/4:
Дробь 1/10:
Приведём 1/10 к знаменателю 20:
1/10 = 2/20.
Это значит, что 1/10 находится на 2-й клетке координатной прямой.
Дробь 1/4:
Приведём 1/4 к знаменателю 20:
1/4 = 5/20.
Это значит, что 1/4 находится на 5-й клетке координатной прямой.
Наносим точки на координатную прямую:
На прямой отметим точки 1/10 (2-я клетка) и 1/4 (5-я клетка).
2. Найдём три дроби, заключённые между 1/10 и 1/4.
Дроби между 1/10 и 1/4:
Располагаются между 2/20 и 5/20. Это дроби со знаменателем 20, у которых числители больше 2, но меньше 5:
3/20,
4/20.
Для разнообразия рассмотрим дроби с другим знаменателем:
Приведём 1/10 и 1/4 к знаменателю 40:
1/10 = 4/40,
1/4 = 10/40.
Дроби между 4/40 и 10/40:
5/40,
6/40,
7/40.
Выбираем три дроби:
Например, 3/20, 4/20 и 7/40.
3. Наносим найденные дроби на координатную прямую.
Приводим дроби к знаменателю 20 (для удобства):
3/20 = 3-я клетка,
4/20 = 4-я клетка,
7/40 = 3.5 клетки (между 3-й и 4-й клетками).
Отмечаем эти точки на прямой.
Математика
