ГДЗ по Математике 5 Класс Номер 772 Дорофеев, Шарыгин, Суворова — Подробные Ответы

На клетчатой бумаге построен квадрат 5 × 5, который разбит на маленькие квадраты (рис. 9.2). Постройте в тетради три разных прямо угольника, имеющие площадь, равную площади закрашенной части квадрата.

Площадь закрашенной части квадрата равна:
5 × 5 — 5 = 25 — 5 = 20 (кв. ед.).

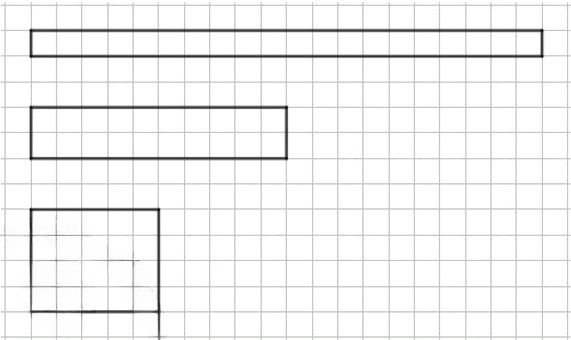
Три разных прямоугольника с площадью 20 кв. ед.:
1 × 20 = 20 (кв. ед.).
2 × 10 = 20 (кв. ед.).
4 × 5 = 20 (кв. ед.).

Площадь закрашенной части квадрата: Исходя из условия, площадь закрашенной части равна 20 квадратным единицам, что вычислено как:
5 × 5 — 5 = 25 — 5 = 20 (кв. ед.).

Необходимость построения прямоугольников: Требуется построить три прямоугольника, каждый из которых имеет площадь 20 квадратных единиц. Для этого используем формулы из условия:

Прямоугольник с размерами 1 × 20;

Прямоугольник с размерами 2 × 10;

Прямоугольник с размерами 4 × 5.

Построение прямоугольников:

Прямоугольник 1 × 20:

Этот прямоугольник представляет собой длинную узкую полосу, состоящую из 1 строки и 20 столбцов. Он занимает ровно 20 клеток.

Прямоугольник 2 × 10:

Этот прямоугольник состоит из 2 строк и 10 столбцов. Он также занимает 20 клеток.

Прямоугольник 4 × 5:

Этот прямоугольник состоит из 4 строк и 5 столбцов, что тоже даёт 20 клеток.

Расположение прямоугольников в тетради:

Постройте прямоугольники на клетчатой бумаге, соблюдая указанные размеры. Каждый прямоугольник должен занимать ровно 20 клеток.