Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 726 Дорофеев, Шарыгин, Суворова — Подробные Ответы
1) Если у вас имеется нелинованная бумага и линейка, но нет угольника или транспортира, то вы можете построить прямоугольник, используя свойства его диагоналей: диагонали прямоугольника равны и точка пересечения диагоналей является серединой каждой из них.
-Начертим отрезок и отметим его середину (рис. 8.32, а).
-Проведём через отмеченную точку прямую и выделим на ней отрезок той же длины, что и первый, причём так, чтобы его середина совпала с серединой первого отрезка (рис. 8.32, б).
-Последовательно соединим концы отрезков (рис. 8.32, в). Полученный четырёхугольник – прямоугольник.
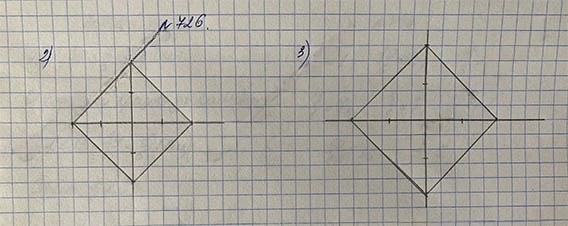
2) Постройте прямоугольник описанным способом на листе нелинованной бумаги.
3) Постройте описанным способом прямоугольник, диагональ которого равна 5 см.
Для построения прямоугольника с использованием свойств диагоналей:
Шаг 1: Построение первой диагонали
- Начертите отрезок длиной 5 см на листе бумаги. Это будет первая диагональ прямоугольника.
- Обозначьте середину отрезка точкой O (рис. 8.32, а).
Шаг 2: Построение второй диагонали
- Проведите прямую линию через точку O, перпендикулярную первой диагонали. Если у вас нет транспортира, можно воспользоваться линейкой и аккуратно на глаз провести перпендикуляр.
- Отметьте на этой линии отрезок той же длины (5 см), чтобы его середина совпала с точкой O. Таким образом, у вас будет вторая диагональ (рис. 8.32, б).
Шаг 3: Соединение концов диагоналей
- Соедините концы первой диагонали с концами второй диагонали последовательно.
- Полученный четырёхугольник будет прямоугольником, так как его диагонали равны и пересекаются в середине (рис. 8.32, в).
Математика
