Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 725 Дорофеев, Шарыгин, Суворова — Подробные Ответы
Начертите два угла с общей вершиной и общей стороной так, чтобы выполнялись следующие условия:
а) ∠AOB = 42°, ∠BOC = 105°, ∠AOC = 147°;
б) ∠AOB = 55°, ∠BOC = 80°, ∠AOC = 25°.
а) ∠AOB = 42°, ∠BOC = 105°, ∠AOC = 147°;
б) ∠AOB = 55°, ∠BOC = 80°, ∠AOC = 25°.
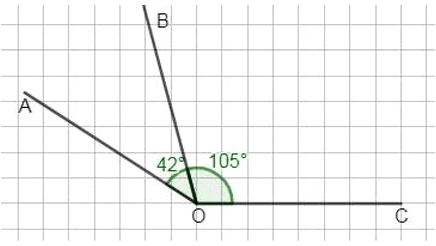
а) Условия:
∠AOB = 42°, ∠BOC = 105°, ∠AOC = 147°.
Проверка:
Сумма ∠AOB + ∠BOC = 42° + 105° = 147°.
Это совпадает с ∠AOC, значит, построение возможно.
Построение:
Нарисуем точку O — вершину углов.
Проведем луч OB.
Построим угол ∠AOB = 42°, отметив точку A с одной стороны от луча OB.
Из той же вершины O построим угол ∠BOC = 105°, отметив точку C с другой стороны от луча OB.
Убедимся, что угол ∠AOC = 147°.
Ответ: Построить углы 42°, 105°, 147° возможно.
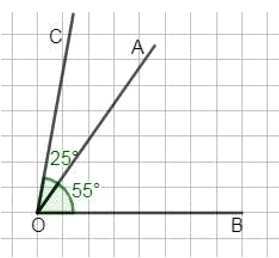
б) Условия:
∠AOB = 55°, ∠BOC = 80°, ∠AOC = 25°.
Проверка:
Здесь ∠AOB + ∠BOC ≠ ∠AOC (55° + 80° = 135°, а ∠AOC = 25°).
Однако это не противоречит построению, так как точки A и C могут находиться по разные стороны от луча OB.
Построение:
Нарисуем точку O — вершину углов.
Проведем луч OB.
Построим угол ∠AOB = 55°, отметив точку A на одной стороне луча OB.
Из той же вершины O построим угол ∠BOC = 80°, отметив точку C на другой стороне от луча OB.
Угол ∠AOC в данном случае будет разностным, то есть ∠AOC = |∠BOC — ∠AOB| = 80° — 55° = 25°.
Ответ: Построить углы 55°, 80°, 25° возможно.
Математика
