Учебник «Математика» для 4-го класса под авторством Г.В. Дорофеева, Т.Н. Мираковой и Т.Б. Буки — это яркий пример современного подхода к обучению, где теория сочетается с практикой, а сложные темы подаются доступно и увлекательно.
Ключевые особенности:
1. Структура и оформление
- Учебник разделен на тематические блоки с постепенным усложнением материала.
- Красочные иллюстрации и схемы помогают визуализировать задачи.
- Каждая тема начинается с «Разминки для ума» — коротких заданий на повторение.
2. Практическая направленность
- Много реальных примеров (расчеты для покупок, измерение площадей и т.д.).
- Задачи разного уровня сложности (от базовых до олимпиадных).
3. Интерактивность
- Включены групповые задания и проекты (например, создание «математического города»).
- Есть рубрика «Проверь себя» для самоконтроля.
5 причин рекомендовать этот учебник:
1. Логичное изложение — от простого к сложному без «провалов» в понимании.
2. Баланс теории и практики — минимум сухих формул, максимум применения.
3. Поддержка интереса — задачи про путешествия, спорт, науку.
4. Гибкость — подходит для разных программ (традиционных и развивающих).
5. Подготовка к ВПР — включает типовые задания для проверочных работ.
Учебник отлично справляется с главной задачей — делает математику понятной и интересной. Он не просто учит считать, но и развивает логику, что пригодится даже вне школы.
P.S. Если ребенок любит головоломки — обратите внимание на раздел «Задачи на смекалку» в конце книги!
Гдз по Математике 4 Класс Часть 1 Страница 6 Дорофеев, Миракова — Подробные ответы
4. По каждому рисунку составь и запиши сумму. Выполни вычисления.
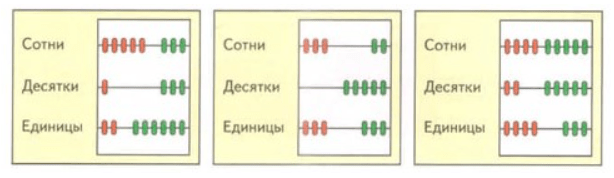
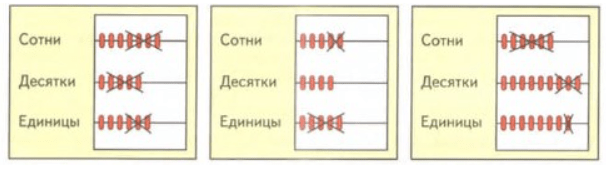
4. 512 + 336 = 848
303 + 253 = 556
424 + 553 = 977
5. По каждому рисунку составь и запиши разность. Выполни действия.
5. 756 — 443 = 313
545 — 204 = 341
698 — 531 = 167
6. В двух мотках было поровну метров провода. От первого мотка отрезали 120 м провода, и в нём осталось 380 м, а от второго мотка отрезали 105 м.
Объясни, что означают выражения:
120 + 105
120 — 105
120 + 380
120 + 380 — 105
6. 120 + 105 = 225 (м) – отрезали провода с двух мотков
120 — 105 = 15 (м) – на 15 м отрезали больше с первого мотка
120 + 380 = 500 (м) – было в первом мотке
120 + 380 — 105 = 395 (м) – осталось во втором мотке
7. Выполни действия.
Сравни выражения в каждой строке. Чем они похожи? Чем различаются? Зависит ли значение выражения от порядка выполнения действия?
70 + 30 ∙ 9 — 5
560 — 240 : 8 + 4
(70 + 30) ∙ 9 — 5
560 — 240 : (8 + 4)
70 + 30 ∙ (9 — 5)
(560 — 240) : 8 + 4
7. 70 + 30 × 9 — 5 = 70 + 270 — 5 = 340 — 5 = 335
(70 + 30) × 9 — 5 = 100 × 9 — 5 = 900 — 5 = 895
70 + 30 × (9 — 5) = 70 + 30 × 4 = 70 + 120 = 210
560 — 240 ÷ 8 + 4 = 560 — 30 + 4 = 530 + 4 = 534
560 + 240 ÷ (8 + 4) = 560 — 240 ÷ 12 = 560 — 20 = 540
(560 — 240) ÷ 8 + 4 = 320 ÷ 8 + 4 = 40 + 4 = 44
Ключевое различие в этих арифметических выражениях заключается в использовании скобок, которые меняют порядок выполнения операций. Это хороший пример того, как небольшие изменения в структуре математического выражения могут привести к совершенно разным результатам.
Давайте более подробно рассмотрим, как порядок выполнения действий влияет на значение этих выражений:
1. В первом выражении 70 + 30 × 9 - 5 = 335 сначала выполняется умножение 30 × 9, затем сложение 70 + 270, и в конце вычитание 340 - 5.
2. Во втором выражении (70 + 30) × 9 - 5 = 895 сначала выполняется сложение в скобках 70 + 30, затем умножение 100 × 9, и в конце вычитание 900 - 5.
3. В третьем выражении 70 + 30 × (9 - 5) = 210 сначала выполняется вычитание в скобках 9 - 5, затем умножение 30 × 4, и в конце сложение 70 + 120.
Таким образом, порядок выполнения действий, определяемый скобками, играет ключевую роль в получении различных результатов, несмотря на использование одних и тех же чисел и арифметических операций.
Это наглядный пример того, как важно правильно расставлять скобки и понимать правила приоритета операций в математике. Такие знания помогают избежать ошибок и получать верные ответы.
8. В коробке лежат 15 шариков: красных, синих и зелёных. Красных шариков в 7 раз больше, чем синих. Сколько зелёных шариков в коробке?
8. 1. Рассмотрим случай, когда в коробке был 1 синий шарик. Тогда количество красных шариков было в 7 раз больше, то есть 7 красных шариков.
2. Чтобы найти количество зеленых шариков, нужно из общего количества шариков (15) вычесть количество синих (1) и красных (7) шариков: 15 — (1 + 7) = 15 — 8 = 7 зеленых шариков.
3. Таким образом, в коробке был 1 синий шарик, 7 красных шариков и 7 зеленых шариков.
Ответ: В коробке было 7 зеленых шариков.
