ГДЗ по Алгебре 9 Класс Проверьте Себя (Тест) Глава 3 Номер 14 Дорофеев, Суворова — Подробные Ответы

Какому промежутку принадлежит положительный корень уравнения $\sqrt{x} = 0,5x^2$?

1) [0; 1]

2) [1; 2]

3) [2; 3]

4) [3; 4]

Уравнение: $\sqrt{x} = 0,5x^2$;

Система уравнений:

$$\begin{cases} y = \sqrt{x} \\ y = 0,5x^2 \end{cases};$$

$y = \sqrt{x}$ — уравнение ветви параболы:

$$\begin{array}{c|c|c|c|c} x & 0 & 1 & 4 & 9 \\ \hline y & 0 & 1 & 2 & 3 \\ \end{array}$$

$y = 0,5x^2$ — уравнение параболы:
$x_0 = 0$ и $y_0 = 0$;

$$\begin{array}{c|c|c|c|c} x & -4 & -2 & 2 & 4 \\ \hline y & 8 & 2 & 2 & 8 \\ \end{array}$$

3) Графики функций:

Положительный корень: $x \in [1; 2]$;

Ответ: 2.

Рассмотрим уравнение:

$$\sqrt{x} = 0,5x^2$$

Для того чтобы решить это уравнение, сначала возведем обе части в квадрат, чтобы избавиться от квадратного корня:

$$x = 0,25x^4$$

Переносим все слагаемые на одну сторону:

$$0,25x^4 — x = 0$$

Вынесем общий множитель $x$:

$$x(0,25x^3 — 1) = 0$$

Таким образом, у нас есть два возможных решения:

$x = 0$

$0,25x^3 — 1 = 0$

Решим второе уравнение:

$$0,25x^3 = 1$$

Умножим обе части на 4:

$$x^3 = 4$$

Теперь найдем кубический корень из обеих сторон:

$$x = \sqrt[3]{4}$$

Таким образом, мы получаем два решения:

$x = 0$ (первое решение)

$x = \sqrt[3]{4}$, что примерно равно 1.587 (второе решение)

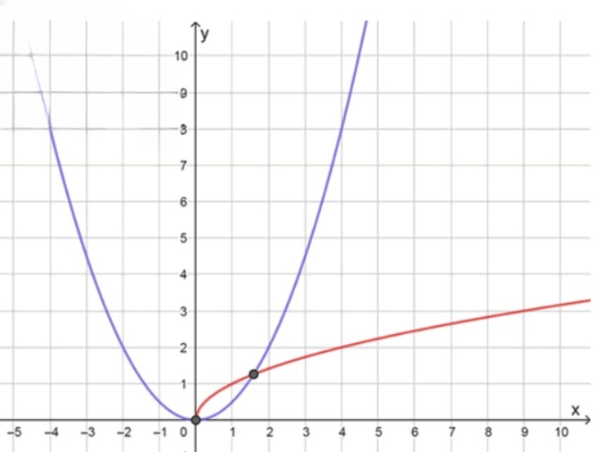
Теперь рассмотрим графики обеих функций $y = \sqrt{x}$ и $y = 0,5x^2$. График функции $y = \sqrt{x}$ представляет собой ветвь параболы, расположенную в первой четверти, так как $\sqrt{x}$ определено только для $x \geq 0$. График функции $y = 0,5x^2$ — это парабола, которая также открывается вверх и имеет вершину в точке $(0, 0)$.

Чтобы найти точку пересечения этих графиков, необходимо приравнять выражения для $y$:

$$\sqrt{x} = 0,5x^2$$

Как мы уже решили, положительный корень уравнения лежит в интервале $[1; 2]$, так как второй корень $\sqrt[3]{4}$ находится в этом промежутке.

Ответ: 2.