ГДЗ по Алгебре 9 Класс Проверьте Себя (Тест) Глава 3 Номер 13 Дорофеев, Суворова — Подробные Ответы

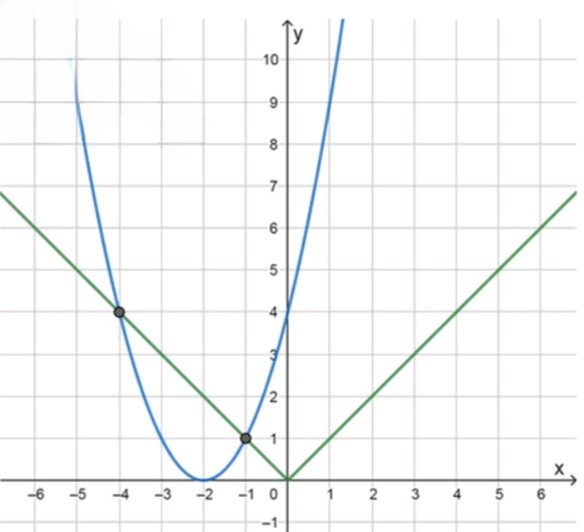
С помощью графиков решите систему уравнений

$$\begin{cases} y = |x| \\ y = (x + 2)^2 \end{cases}.$$

$$\begin{cases} y = |x| \\ y = (x + 2)^2 \end{cases}:$$

$y = |x|$ — уравнение графика модуля:

$$\begin{array}{c|c|c|c} x & -1 & 0 & 1 \\ \hline y & 1 & 0 & 1 \end{array}$$

$y = (x + 2)^2$ — уравнение параболы:
$x_0 = -2$ и $y_0 = 0$;

$$\begin{array}{c|c|c|c|c|c|c} x & -5 & -4 & -3 & -1 & 0 & 1 \\ \hline y & 9 & 4 & 1 & 1 & 4 & 9 \end{array}$$

3) Графики функций:

Ответ: $(-4; 4)$ и $(-1; 1)$.

Рассмотрим первое уравнение системы:

$$y = |x|$$

Это уравнение описывает график модуля. График функции $y = |x|$ представляет собой «V»-образную фигуру, где для всех $x \geq 0$, $y = x$, а для всех $x < 0$, $y = -x$. Это отражение линии $y = x$ относительно оси $x$. Рассмотрим несколько значений $x$:

При $x = -1$, $y = |-1| = 1$

При $x = 0$, $y = |0| = 0$

При $x = 1$, $y = |1| = 1$

Таблица для функции $y = |x|$ будет следующей:

$$\begin{array}{c|c|c|c} x & -1 & 0 & 1 \\ \hline y & 1 & 0 & 1 \end{array}$$

Рассмотрим второе уравнение системы:

$$y = (x + 2)^2$$

Это уравнение описывает параболу, открывающуюся вверх. Парабола с вершиной в точке $(-2, 0)$ является смещением стандартной параболы $y = x^2$ на 2 единицы влево по оси $x$. Для нескольких значений $x$:

При $x = -5$, $y = (-5 + 2)^2 = (-3)^2 = 9$

При $x = -4$, $y = (-4 + 2)^2 = (-2)^2 = 4$

При $x = -3$, $y = (-3 + 2)^2 = (-1)^2 = 1$

При $x = -1$, $y = (-1 + 2)^2 = (1)^2 = 1$

При $x = 0$, $y = (0 + 2)^2 = 2^2 = 4$

При $x = 1$, $y = (1 + 2)^2 = 3^2 = 9$

Таблица для функции $y = (x + 2)^2$ будет следующей:

$$\begin{array}{c|c|c|c|c|c|c} x & -5 & -4 & -3 & -1 & 0 & 1 \\ \hline y & 9 & 4 & 1 & 1 & 4 & 9 \end{array}$$

Теперь рассмотрим графики этих двух функций. График функции $y = |x|$ представляет собой «V»-образную кривую, а график функции $y = (x + 2)^2$ — параболу, открывающуюся вверх. Эти два графика пересекаются в точках, где их значения $y$ равны друг другу. То есть, нужно решить уравнение:

$$|x| = (x + 2)^2$$

Рассмотрим два случая: $x \geq 0$ и $x < 0$.

• Когда $x \geq 0$, $|x| = x$, тогда уравнение становится:

$$x = (x + 2)^2$$

Решим это уравнение:

$$x = x^2 + 4x + 4$$

Переносим все на одну сторону:

$$x^2 + 3x + 4 = 0$$

Решение этого уравнения не дает действительных корней, так как дискриминант $D = 3^2 — 4 \cdot 1 \cdot 4 = 9 — 16 = -7$, что означает отсутствие решений в данной области.

• Когда $x < 0$, $|x| = -x$, тогда уравнение становится:

$$-x = (x + 2)^2$$

Решим это уравнение:

$$-x = x^2 + 4x + 4$$

Переносим все на одну сторону:

$$x^2 + 5x + 4 = 0$$

Решим это квадратное уравнение с использованием формулы для корней:

$$x = \frac{-5 \pm \sqrt{5^2 — 4 \cdot 1 \cdot 4}}{2 \cdot 1} = \frac{-5 \pm \sqrt{25 — 16}}{2} = \frac{-5 \pm \sqrt{9}}{2} = \frac{-5 \pm 3}{2}$$

Таким образом, получаем два решения:

$$x_1 = \frac{-5 + 3}{2} = -1 \quad \text{и} \quad x_2 = \frac{-5 — 3}{2} = -4$$

Теперь находим ординаты для этих значений $x$. Для $x_1 = -1$:

$$y_1 = |x_1| = 1$$

Для $x_2 = -4$:

$$y_2 = |x_2| = 4$$

Ответ: $(-4; 4)$ и $(-1; 1)$.