ГДЗ по Алгебре 9 Класс Проверьте Себя (Тест) Глава 3 Номер 12 Дорофеев, Суворова — Подробные Ответы

Для каждой системы уравнений укажите число её решений (используйте графические соображения).

А) $\begin{cases} y = \frac{2}{x} \\ y = -5x \end{cases}$

Б) $\begin{cases} y = \frac{2}{x} \\ y = 5 — x \end{cases}$

В) $\begin{cases} y = \frac{2}{x} \\ y = 5 \end{cases}$

1) 1 решение

2) 2 решения

3) 3 решения

4) нет решений

А) $\begin{cases} y = \frac{2}{x} \\ y = -5x \end{cases}$

$y = \frac{2}{x}$ — уравнение гиперболы:
$a > 0$, значит график лежит в I и III четвертях;
Уравнения асимптот: $x = 0$ и $y = 0$;

$y = -5x$ — уравнение прямой:
$a < 0$, значит функция убывает;
График пересекает ось $x$ в точке с абсциссой: $x = 0$;
График пересекает ось $y$ в точке с ординатой: $y = 0$;

3) Схематический рисунок:

Графики не пересекаются — решений нет;

Б) $\begin{cases} y = \frac{2}{x} \\ y = 5 — x \end{cases}$

$y = \frac{2}{x}$ — уравнение гиперболы:
$a > 0$, значит график лежит в I и III четвертях;
Уравнения асимптот: $x = 0$ и $y = 0$;

$y = 5 — x$ — уравнение прямой:
$a < 0$, значит функция убывает;
График пересекает ось $x$ в точке с абсциссой: $x = 5$;
График пересекает ось $y$ в точке с ординатой: $y = 5$;

3) Схематический рисунок:

Графики пересекаются в двух точках — 2 решения;

В) $\begin{cases} y = \frac{2}{x} \\ y = 5 \end{cases}$

$y = \frac{2}{x}$ — уравнение гиперболы:
$a > 0$, значит график лежит в I и III четвертях;
Уравнения асимптот: $x = 0$ и $y = 0$;

$y = 5$ — уравнение прямой;

3) Схематический рисунок:

Графики пересекаются в одной точке — 1 решение;

Ответ: А) 4; Б) 2; В) 1.

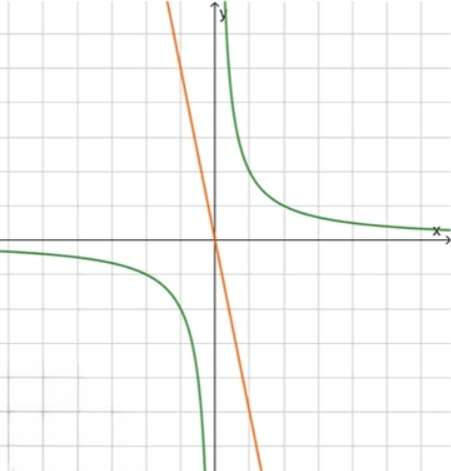
А) $\begin{cases} y = \frac{2}{x} \\ y = -5x \end{cases}$

Рассмотрим первое уравнение $y = \frac{2}{x}$. Это уравнение описывает гиперболу, у которой асимптоты — оси $x$ и $y$. График гиперболы будет располагаться в первой и третьей четвертях координатной плоскости, так как коэффициент при $x$ положительный. Это связано с тем, что $a > 0$ в уравнении $y = \frac{2}{x}$, что означает, что график гиперболы будет иметь два ответвления, одно в первой и другое в третьей четверти.

Рассмотрим второе уравнение $y = -5x$. Это уравнение прямой, наклон которой отрицателен, так как коэффициент при $x$ отрицателен ($a < 0$). Прямая будет убывать, то есть с увеличением $x$ значение $y$ будет уменьшаться. Прямая пересекает ось $x$ в точке с абсциссой $x = 0$, и ось $y$ в точке с ординатой $y = 0$.

Схематический рисунок графиков гиперболы и прямой показывает, что эти графики не пересекаются. График гиперболы находится в другой области координатной плоскости по сравнению с графиком прямой. Таким образом, решений нет.

Ответ: 4.

Б) $\begin{cases} y = \frac{2}{x} \\ y = 5 — x \end{cases}$

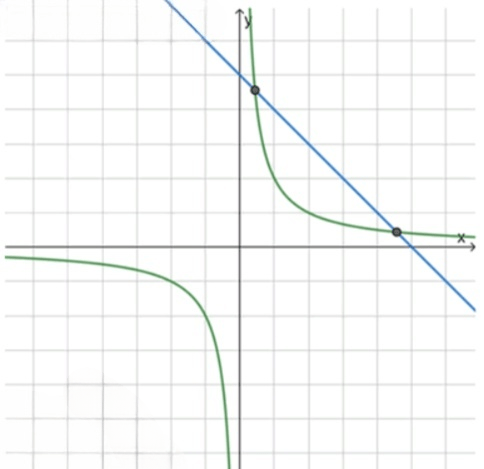
Рассмотрим первое уравнение $y = \frac{2}{x}$, которое, как уже отмечалось, является уравнением гиперболы с асимптотами на осях $x$ и $y$. График гиперболы будет располагаться в первой и третьей четвертях координатной плоскости, как указано ранее.

Рассмотрим второе уравнение $y = 5 — x$. Это уравнение прямой с наклоном $a = -1$, то есть прямая будет убывать. Прямая пересекает ось $x$ в точке $x = 5$, а ось $y$ — в точке $y = 5$. Поскольку график прямой наклонен вниз, она будет иметь одно пересечение с графиком гиперболы в первой и одно в третьей четвертях, где оба графика пересекаются.

Схематический рисунок графиков гиперболы и прямой показывает, что они пересекаются в двух точках — одна в первой четверти, а другая в третьей.

Ответ: 2.

В) $\begin{cases} y = \frac{2}{x} \\ y = 5 \end{cases}$

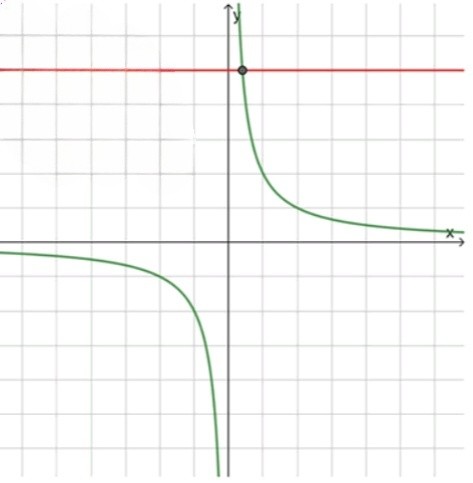
Рассмотрим первое уравнение $y = \frac{2}{x}$, которое описывает гиперболу с асимптотами на осях $x$ и $y$. График гиперболы лежит в первой и третьей четвертях координатной плоскости.

Рассмотрим второе уравнение $y = 5$, которое представляет собой горизонтальную прямую, проходящую через точку $y = 5$. Эта прямая пересекает ось $y$ в точке с ординатой $y = 5$ и не имеет угла наклона, так как это горизонтальная линия.

Схематический рисунок показывает, что график гиперболы и горизонтальная прямая пересекаются в одной точке, так как гипербола проходит через точку $y = 5$, в отличие от прямой, которая имеет фиксированное значение $y = 5$. Таким образом, графики пересекаются в одной точке.

Ответ: 1.