ГДЗ по Алгебре 9 Класс Проверьте Себя (Тест) Глава 2 Номер 15 Дорофеев, Суворова — Подробные Ответы

Для каждого неравенства укажите множество его решений.

А) $x^2 — 25 \leq 0$
Б) $x^2 + 25 \leq 0$
В) $x^2 — 25 \geq 0$
Г) $x^2 + 25 \geq 0$

$(-\infty; +\infty)$

$[-5; 5]$

$(-\infty; -5] \cup [5; +\infty)$

$\varnothing$

А) $x^2 — 25 \leq 0$:
$(x — 5)(x + 5) \leq 0$;
Нули функции:
$x_1 — 5 = 0$, отсюда $x_1 = 5$;
$x_2 + 5 = 0$, отсюда $x_2 = -5$;
Значения на интервалах:

Ответ: $x \in [-5; 5]$;

Б) $x^2 — 25 \geq 0$:
$(x — 5)(x + 5) \geq 0$;
Нули функции:
$x_1 — 5 = 0$, отсюда $x_1 = 5$;
$x_2 + 5 = 0$, отсюда $x_2 = -5$;
Значения на интервалах:

Ответ: $x \in (-\infty; -5] \cup [5; +\infty)$;

В) $x^2 + 25 \leq 0$:
$x^2 \leq -25$ — решений нет;
Ответ: $\varnothing$;

Г) $x^2 + 25 \geq 0$:
$x^2 \geq -25$ — верно всегда;
Ответ: $(-\infty; +\infty)$;

Ответ: А) 2; Б) 3; В) 4; Г) 1.

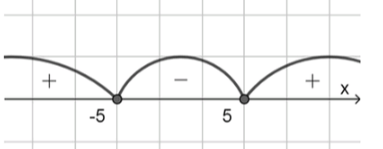
А) Неравенство: $x^2 — 25 \leq 0$

Перепишем в виде произведения:
$x^2 — 25 = (x — 5)(x + 5)$, следовательно:
$(x — 5)(x + 5) \leq 0$

Найдём нули функции:
$x — 5 = 0 \Rightarrow x = 5$
$x + 5 = 0 \Rightarrow x = -5$

Это границы интервалов, на которых знак выражения может меняться.
Разметим числовую прямую:
интервалы: $(-\infty; -5)$, $(-5; 5)$, $(5; +\infty)$

Проверим знак выражения на каждом интервале:
— при $x < -5$, например $x = -6$:
$(-6 — 5)(-6 + 5) = (-11)(-1) = 11 > 0$
— при $x \in (-5; 5)$, например $x = 0$:
$(0 — 5)(0 + 5) = (-5)(5) = -25 < 0$
— при $x > 5$, например $x = 6$:
$(6 — 5)(6 + 5) = (1)(11) = 11 > 0$

Нам нужно, чтобы произведение было меньше либо равно нуля, то есть неположительным.
Такое происходит на промежутке от $-5$ до $5$, включая границы, поскольку на границах выражение обращается в ноль.

Ответ: $x \in [-5; 5]$

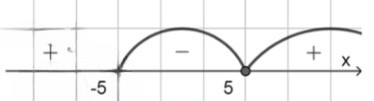
Б) Неравенство: $x^2 — 25 \geq 0$

Представим снова как произведение:
$x^2 — 25 = (x — 5)(x + 5) \Rightarrow (x — 5)(x + 5) \geq 0$

Те же нули: $x = -5$ и $x = 5$
Анализ интервалов тот же, знаки также:
— $(-\infty; -5)$: положительное
— $(-5; 5)$: отрицательное
— $(5; +\infty)$: положительное

Нам требуется, чтобы выражение было больше либо равно нулю, то есть положительное или равное нулю. Это выполняется на концах и за пределами интервала от $-5$ до $5$:

Ответ: $x \in (-\infty; -5] \cup [5; +\infty)$

В) Неравенство: $x^2 + 25 \leq 0$

Левая часть: $x^2 + 25$. Заметим, что $x^2 \geq 0$ при любом $x$, а значит:
$x^2 + 25 \geq 25$ всегда. Это выражение строго положительное для всех $x \in \mathbb{R}$.

Следовательно, оно никогда не будет меньше или равно нулю.

Ответ: $\varnothing$

Г) Неравенство: $x^2 + 25 \geq 0$

Аналогично: $x^2 \geq 0$, и $x^2 + 25 \geq 25$, то есть всегда положительно.

Поскольку выражение $x^2 + 25$ положительно при любом $x$, неравенство выполняется при всех вещественных значениях.

Ответ: $x \in (-\infty; +\infty)$

Окончательные соответствия:
А) 2
Б) 3
В) 4
Г) 1