ГДЗ по Алгебре 9 Класс Повторите Математику (По курсу 5-8 классов) Номер 72 Дорофеев, Суворова — Подробные Ответы

В одной системе координат постройте графики функций и найдите координаты их точек пересечения:

а) $y = -\frac{1}{x}$ и $y = -x$;
б) $y = \frac{2}{x}$ и $y = x + 1$.

Точки пересечения:

а) $y = -\frac{1}{x}$, $y = -x$;
Графики функций:

Ответ: $(-1; 1); (1; -1)$.

б) $y = \frac{2}{x}$, $y = x + 1$;
Графики функций:

Ответ: $(-2; -1); (1; 2)$.

Точки пересечения:

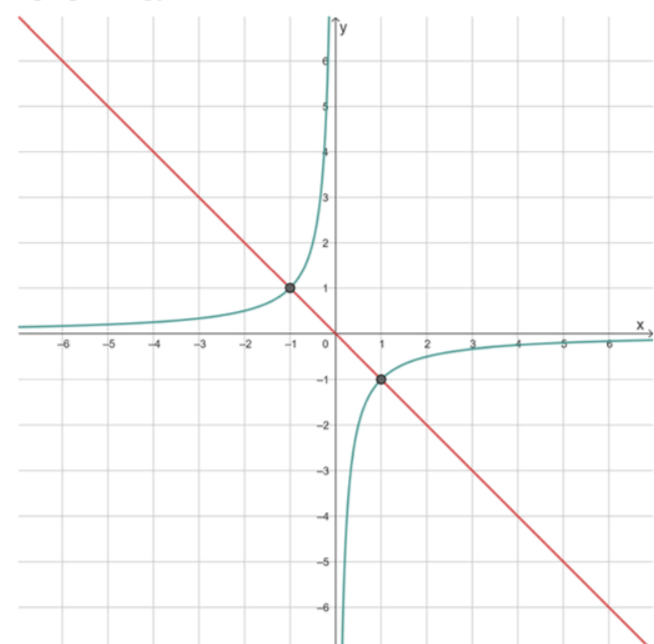
а) даны функции $y = -\frac{1}{x}$ и $y = -x$. Для нахождения координат точек пересечения приравняем правые части уравнений:
$-\frac{1}{x} = -x$.

Умножим обе части уравнения на $x$ (при условии, что $x \ne 0$):
$-1 = -x^2$.

Переносим знак «минус»:
$x^2 = 1$.

Извлекаем квадратный корень:
$x = \pm 1$.

Подставляем найденные значения $x$ в функцию $y = -x$, чтобы найти соответствующие значения $y$.

При $x = 1$:
$y = -1$.

При $x = -1$:
$y = 1$.

Следовательно, точки пересечения имеют координаты $(-1; 1)$ и $(1; -1)$.

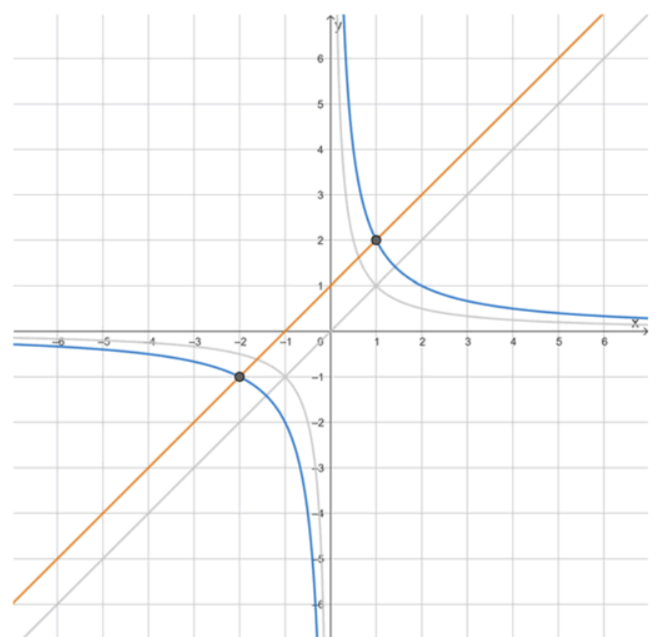
б) даны функции $y = \frac{2}{x}$ и $y = x + 1$. Для нахождения координат точек пересечения приравняем правые части уравнений:
$\frac{2}{x} = x + 1$.

Умножим обе части уравнения на $x$ (при условии, что $x \ne 0$):
$2 = x^2 + x$.

Приведем уравнение к стандартному виду квадратного уравнения:
$x^2 + x — 2 = 0$.

Вычислим дискриминант:
$D = 1^2 — 4 \cdot 1 \cdot (-2) = 1 + 8 = 9$.

Находим корни уравнения:
$x_1 = \frac{-1 — 3}{2} = \frac{-4}{2} = -2$,
$x_2 = \frac{-1 + 3}{2} = \frac{2}{2} = 1$.

Теперь подставим найденные значения $x$ в функцию $y = x + 1$.

При $x = -2$:
$y = -2 + 1 = -1$.

При $x = 1$:
$y = 1 + 1 = 2$.

Таким образом, точки пересечения имеют координаты $(-2; -1)$ и $(1; 2)$.

Окончательный результат:
а) $(-1; 1); (1; -1)$.
б) $(-2; -1); (1; 2)$.