
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Повторите Математику (По курсу 5-8 классов) Номер 71 Дорофеев, Суворова — Подробные Ответы
Постройте график функции:
а) ;
б) .
По графику определите:
1) возрастает или убывает функция при ; при ;
2) на каком промежутке значения функции положительны; отрицательны.
Построить график:
а) , , ;
1) Функция убывает;
при ;
при ;
б) , , ;
Свойства функции:
1) Функция возрастает;
при ;
при ;
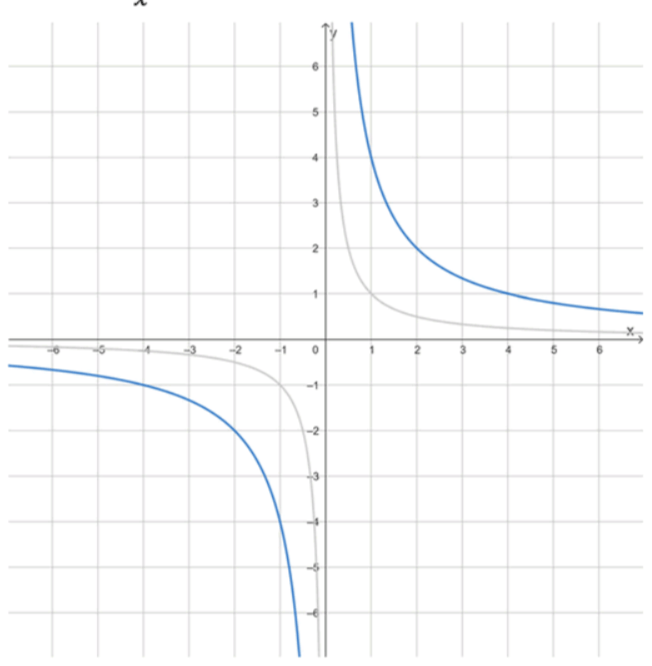
а) .
Эта функция имеет вид , где . Так как значение параметра положительное (), график функции представляет собой гиперболу, расположенную в первой и третьей координатных четвертях. Область определения функции: все действительные значения , кроме точки , так как в этой точке функция не определена. Следовательно, . Значения функции также не принимают ноль, поэтому область значений: .
Свойства функции:
Так как , функция является убывающей на каждом из промежутков области определения. Это означает, что при увеличении значения функции уменьшаются как на промежутке , так и на промежутке . Например, при , , при , , при , . Аналогично, при , , при , , при , . Таким образом, чем больше по модулю , тем ближе значение функции к нулю.
Знак функции определяется знаком переменной . При числитель и знаменатель имеют одинаковый знак, поэтому . При знаменатель отрицателен, а числитель положителен, поэтому . Следовательно: при ; при .
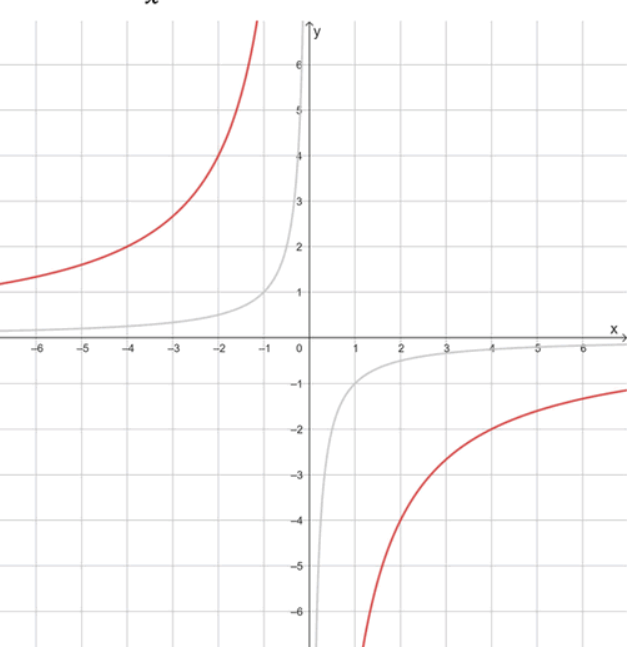
б) .
Эта функция также имеет вид , но в данном случае . Так как параметр отрицателен (), график функции представляет собой гиперболу, расположенную во второй и четвертой координатных четвертях. Область определения функции: все действительные значения , кроме нуля, то есть . Область значений аналогична: .
Свойства функции:
Так как , функция является возрастающей на каждом из промежутков своей области определения. Это означает, что если увеличивается, то также увеличивается на промежутках и . Например, для положительных : при , ; при , ; при , . Значения становятся ближе к нулю, то есть увеличиваются. Для отрицательных : при , ; при , ; при , . Здесь также значения увеличиваются по мере увеличения .
Знак функции противоположен знаку , так как числитель отрицателен, а знаменатель принимает как положительные, так и отрицательные значения. При знаменатель положителен, поэтому функция отрицательна: при . При знаменатель отрицателен, поэтому произведение отрицательного числителя и отрицательного знаменателя положительно: при .
Итог:
а) — убывающая функция, при , при .
б) — возрастающая функция, при , при .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!