ГДЗ по Алгебре 9 Класс Повторите Математику (По курсу 5-8 классов) Номер 70 Дорофеев, Суворова — Подробные Ответы

Графиком какой из функций: $y = \frac{1}{3}x$, $y = \frac{x}{3}$, $y = \frac{3}{x}$ — является гипербола? Постройте эту гиперболу.

Является гиперболой:
$y = \frac{k}{x}$, $y = \frac{3}{x}$, $k = 3$, $k > 0$;

График данной функции:

Ответ: $y = \frac{3}{x}$.

Является гиперболой:

Общая форма уравнения функции обратной пропорциональности записывается как $y = \frac{k}{x}$, где $k$ — это коэффициент, который определяет, как именно расположена гипербола на координатной плоскости, её «растянутость» и в каких четвертях она будет находиться.

Из предложенных функций рассмотрим каждую:

$y = \frac{1}{3}x$. Данная функция имеет вид $y = kx$, где $k = \frac{1}{3}$. Это линейная функция, её графиком является прямая линия, проходящая через начало координат с угловым коэффициентом $k = \frac{1}{3}$. Следовательно, эта функция не является гиперболой, а является прямой.

$y = \frac{x}{3}$. Эта функция аналогична предыдущей, так как её можно записать в виде $y = kx$, где $k = \frac{1}{3}$. Следовательно, её графиком также является прямая, проходящая через начало координат. Это тоже не гипербола, а линейная функция.

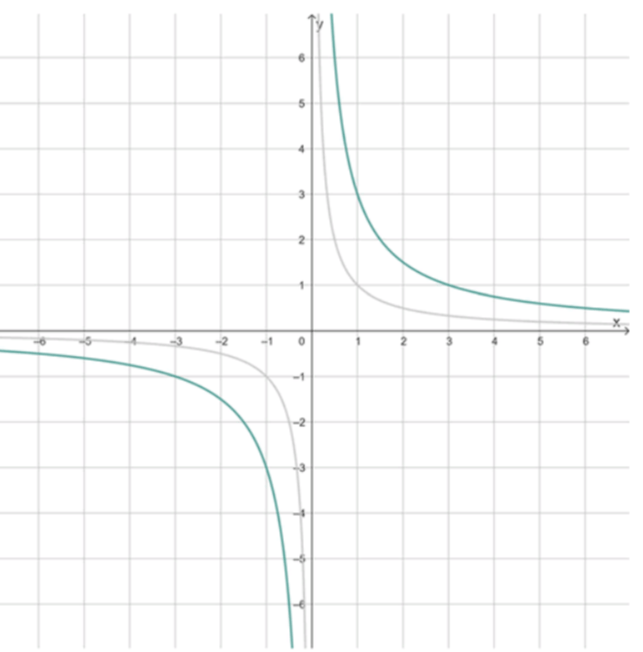
$y = \frac{3}{x}$. Эта функция имеет вид $y = \frac{k}{x}$, где $k = 3$. Это соответствует определению обратной пропорциональности, графиком которой является гипербола. Здесь $k = 3 > 0$, поэтому ветви гиперболы будут расположены в I и III координатных четвертях, так как при $x > 0$ значение $y$ также положительно, а при $x < 0$ значение $y$ отрицательно.

Таким образом, среди данных функций гиперболой является именно $y = \frac{3}{x}$.

График данной функции представляет собой две ветви гиперболы:
— первая ветвь находится в I четверти (при $x > 0$, $y > 0$);
— вторая ветвь находится в III четверти (при $x < 0$, $y < 0$).

Ответ: $y = \frac{3}{x}$.