
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Повторите Математику (По курсу 5-8 классов) Номер 66 Дорофеев, Суворова — Подробные Ответы
Постройте график функции:
а)
б)
в)
г)
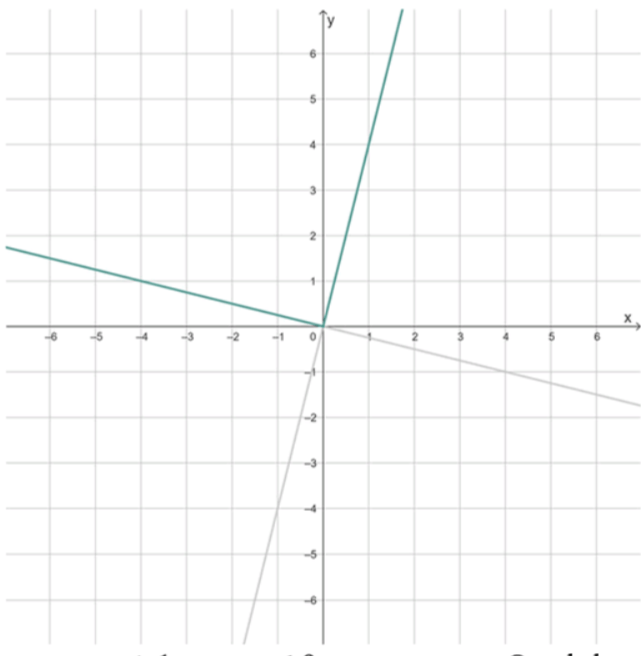
а) .
Здесь функция задана кусочно: при всех отрицательных и нулевых значениях аргумента используется формула , а при положительных значениях аргумента используется формула . Формула является линейной функцией с коэффициентом наклона , который меньше нуля, следовательно, эта функция убывает. Прямая проходит через точку , так как подстановка даёт . Наклон линии очень пологий, так как модуль коэффициента равен . Для примера, если взять , то , значит точка лежит на графике. Если взять , то , точка . Таким образом, часть графика для — это убывающая прямая через начало координат, уходящая влево вверх. Вторая часть, при , описывается уравнением . Здесь коэффициент наклона , функция возрастает, наклон очень крутой. Она также проходит через начало координат. Например, при , ; при , . График состоит из двух лучей: левый луч убывающий, правый луч возрастающий.
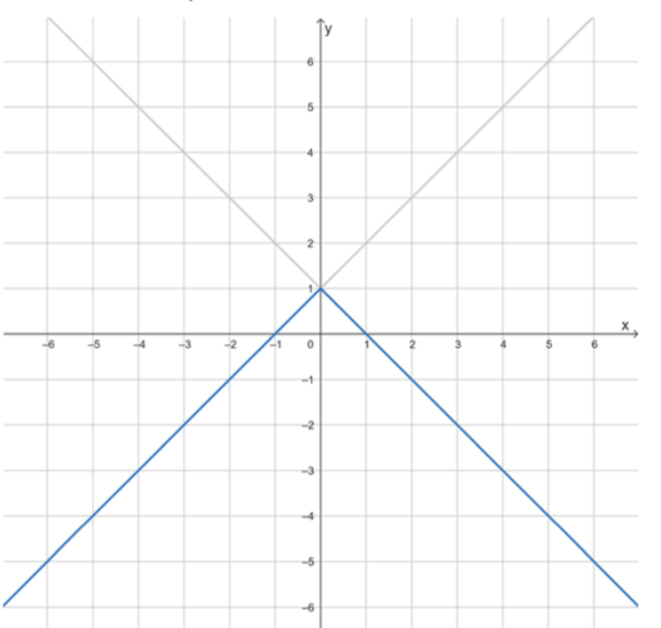
б) .
Здесь также кусочная функция. Для формула задаёт прямую с коэффициентом наклона , то есть возрастающую функцию. Она пересекает ось ординат в точке , а также проходит через точку . Следовательно, часть графика для — возрастающий луч, направленный влево вниз и проходящий через точку . Для формула задаёт прямую с угловым коэффициентом , то есть убывающую. Она также пересекает ось ординат в точке , а ось абсцисс — в точке . Таким образом, часть графика при — убывающий луч, уходящий вправо вниз. В результате график представляет собой букву V, вершина которой находится в точке .
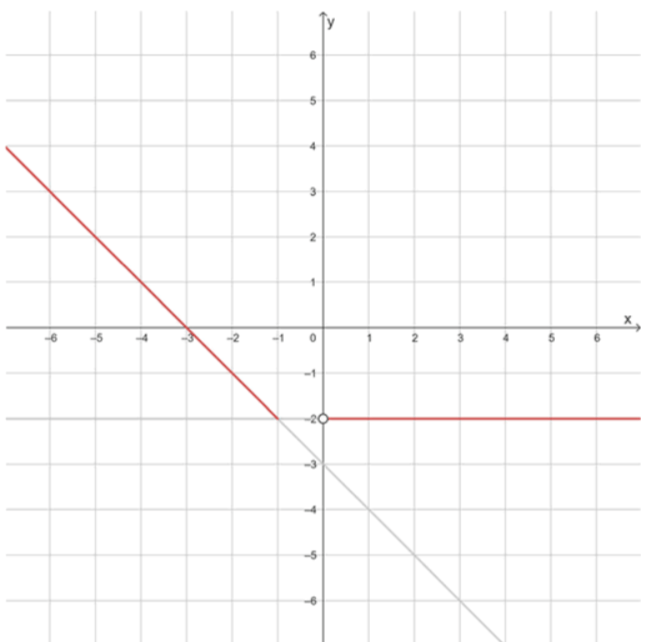
в) .
В этом случае для значений функция задаётся формулой . Это линейная функция с угловым коэффициентом , то есть убывающая. Она пересекает ось ординат в точке , а также проходит через точку . Но область применения ограничена , поэтому берём часть этой прямой, которая находится левее или равна . Для проверки: при значение функции , то есть точка принадлежит графику. Таким образом, левая ветвь графика — это убывающий луч, начиная от точки и уходящий влево вверх. Для значение функции постоянно равно . Это значит, что график на интервале представляет собой горизонтальный луч, параллельный оси абсцисс, расположенный на высоте , начиная с точки и уходящий вправо.
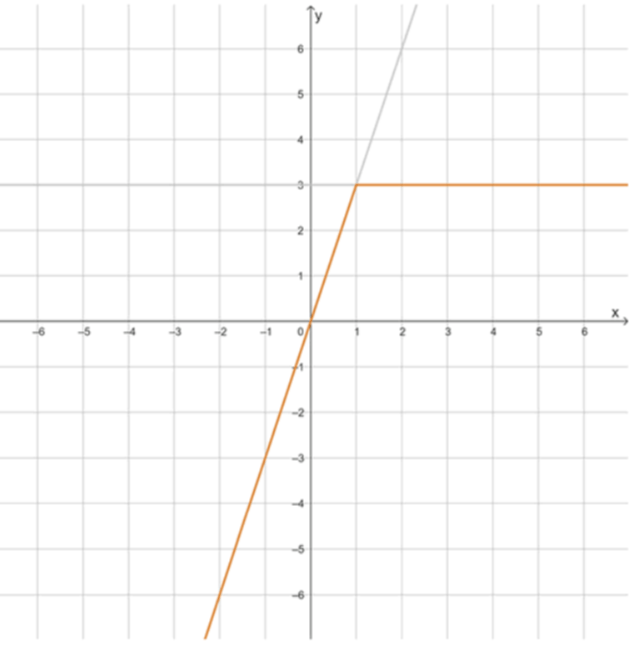
г) .
Здесь для функция имеет вид , что является линейной зависимостью с коэффициентом наклона , значит функция возрастает. Она проходит через начало координат и через точку . График этой части — это луч прямой, направленный влево вниз и вправо вверх до точки . Для функция принимает постоянное значение . Это горизонтальная прямая, параллельная оси абсцисс, начинающаяся в точке и продолжающаяся вправо.
Таким образом:
— в пункте а график состоит из двух прямых с разным наклоном, пересекающихся в начале координат;
— в пункте б график имеет вид угла или буквы V;
— в пункте в график объединяет убывающий луч слева и горизонтальный луч справа;
— в пункте г график объединяет возрастающую прямую до точки и горизонтальный луч на уровне .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!