
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Повторите Математику (По курсу 5-8 классов) Номер 65 Дорофеев, Суворова — Подробные Ответы
Постройте график линейной функции. В каждом случае укажите:
1) возрастающей или убывающей является функция;
2) координаты точки пересечения графика функции с осью абсцисс, с осью ординат;
3) при каких значениях х функция принимает положительные значения, отрицательные значения:
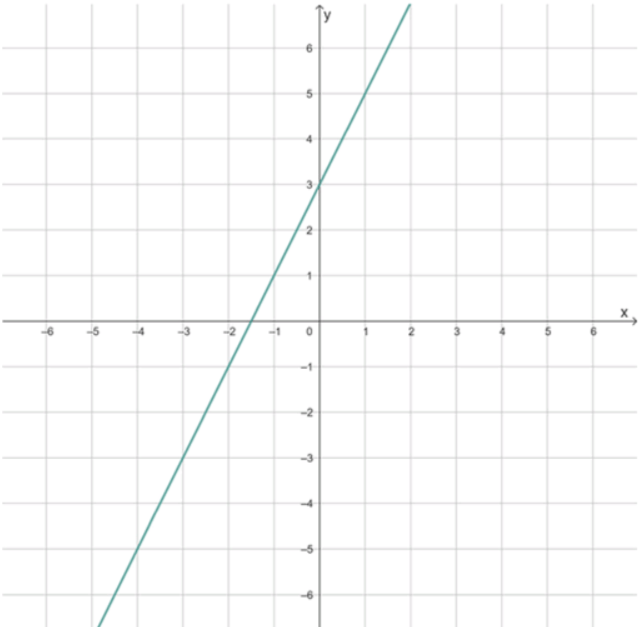
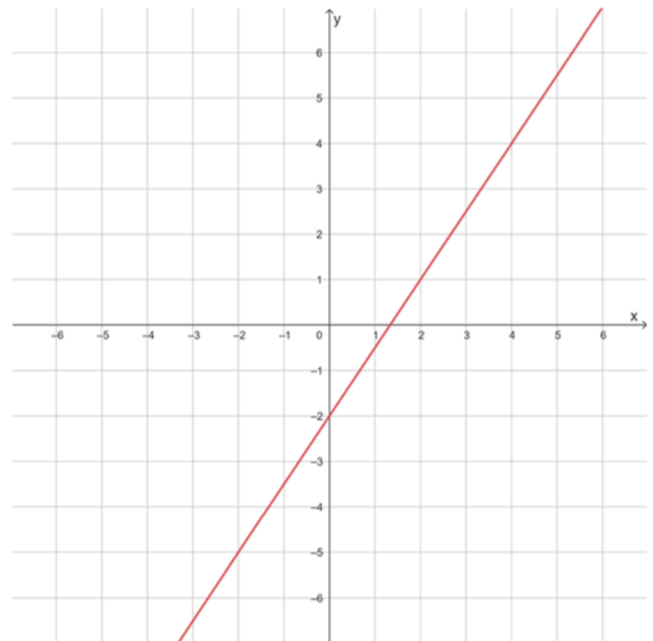
а) y=2x+3; в) y=1,5x-2; д) y=1,2x;
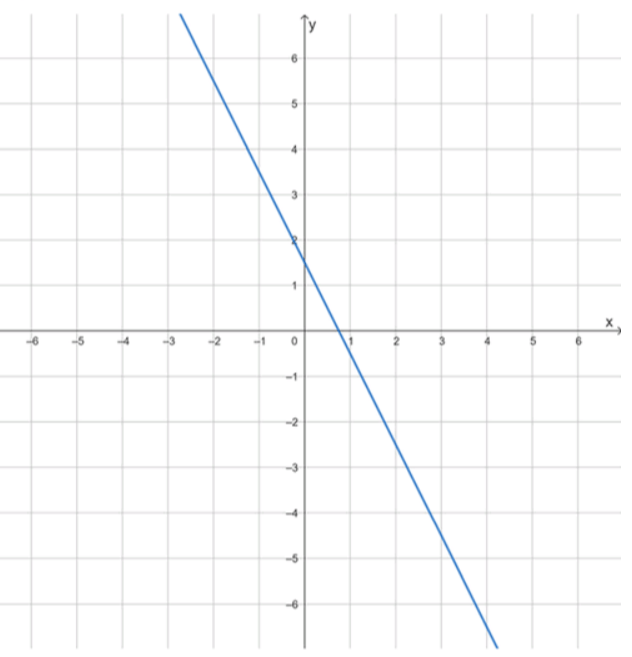
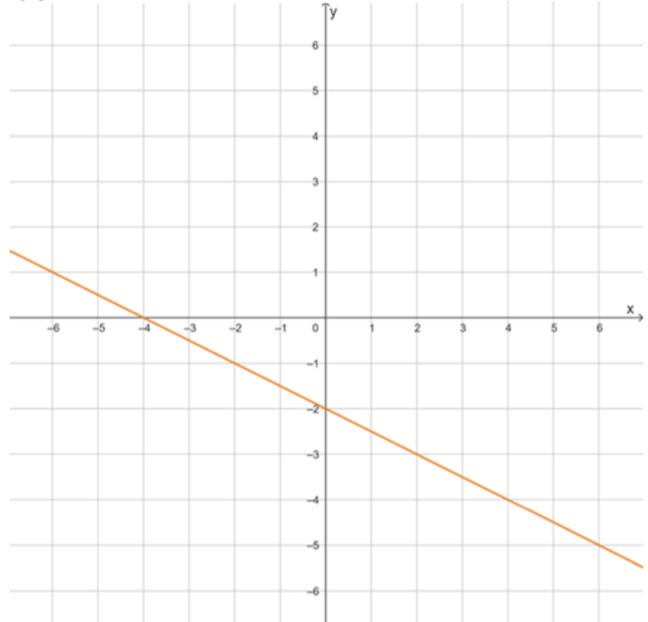
б) y=-2x+1,5; г) y=-0,5x-2; е) y=-0,7x.
Построить график:
а) , , ;
Свойства функции:
1) Функция возрастает;
2) Точки и ;
при ;
при ;
б) , , ;
Свойства функции:
1) Функция убывает;
2) Точки и ;
при ;
при ;
в) , , ;
Свойства функции:
1) Функция возрастает;
2) Точки и ;
при ;
при ;
г) , , ;
Свойства функции:
1) Функция убывает;
2) Точки и ;
при ;
при ;
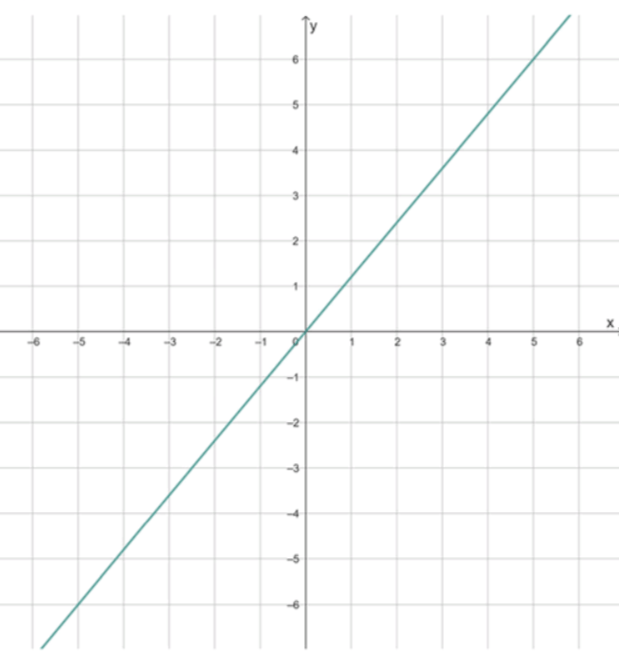
д) , , ;
Свойства функции:
1) Функция возрастает;
2) Есть одна точка ;
при ;
при ;
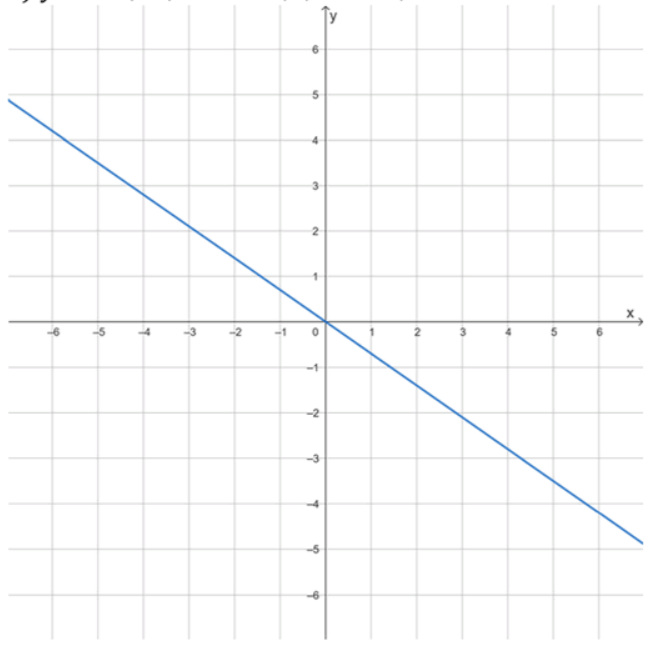
е) , , ;
Свойства функции:
1) Функция убывает;
2) Есть одна точка ;
при ;
при ;
а) , , .
Так как угловой коэффициент положительный, функция является возрастающей, её график — прямая, идущая снизу вверх. Найдём точки пересечения с осями координат. Для оси ординат: при имеем , точка . Для оси абсцисс: решаем , получаем , точка . Таким образом, график проходит через эти точки. Теперь определим знаки функции: при значение положительно, то есть при . При значение функции отрицательно, то есть при .
б) , , .
Так как угловой коэффициент отрицательный, функция является убывающей, её график идёт сверху вниз. Найдём точки пересечения. При получаем , точка . Для пересечения с осью абсцисс: решаем , получаем , точка . Для знаков функции: при значение положительно, то есть при . При значение отрицательно, то есть при
в) , , .
Так как положительное, функция возрастает. При имеем , точка . Для пересечения с осью абсцисс решаем , получаем , точка . Определим области знаков: при значение функции положительно, то есть при . При значение функции отрицательно, то есть при .
г) , , .
Так как коэффициент отрицательный, функция убывает. При получаем , точка . Для нахождения пересечения с осью абсцисс решаем уравнение , получаем , точка . Теперь по знакам: если , то значение положительное, то есть при . Если , то функция отрицательна, то есть при .
д) , , .
Поскольку коэффициент положительный, функция возрастает. Прямая проходит через начало координат, так как при имеем . Следовательно, точка пересечения с осями только одна: . Для знаков: при значение функции положительно, то есть при . При значение отрицательно, то есть при .
е) , , .
Поскольку коэффициент отрицательный, функция убывает. При имеем , значит, точка . Это единственная точка пересечения с осями координат. Для анализа знаков: если , то подстановка даёт , а так как отрицательно, произведение становится положительным, значит при . Если , то произведение отрицательное, значит при .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!