
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 9 Дорофеев, Суворова — Подробные Ответы
Изобразите на координатной прямой множество точек, координаты которых удовлетворяют данному условию, и запишите его на символическом языке:
а) ; в) ; д) ;
б) ; г) ; е) .
Образец.
— расстояние от точки до точки 6 не превосходит 2 (рис. 1.4, а);
— расстояние от точки до точки 6 больше 2 (рис. 1.4, б).
а) :
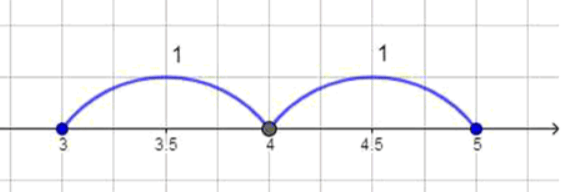
Расстояние от точки до точки не превосходит ;
Ответ: .
б) :
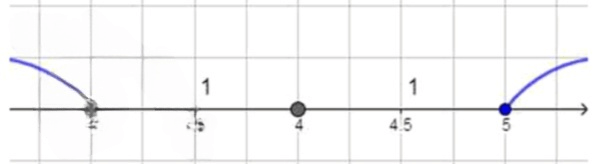
Расстояние от точки до точки не меньше ;
Ответ: .
в) :
Расстояние от точки до точки меньше ;
Ответ: .
г) :
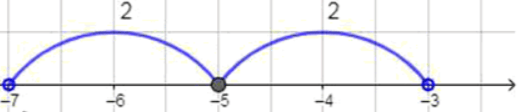
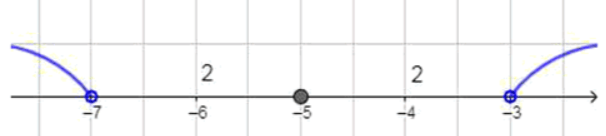
Расстояние от точки до точки больше ;
Ответ: .
д) :
Расстояние от точки до точки не больше ;
Ответ: .
е) :
а) Условие означает, что расстояние от произвольной точки с координатой до фиксированной точки с координатой на координатной прямой не превосходит единицы. То есть если взять точку и отмерить влево и вправо по , мы получим интервал от до , включающий концы, так как неравенство нестрогое (). Следовательно, множество решений записывается как .
б) Условие означает, что расстояние от точки до точки на координатной прямой не меньше единицы. Это значит, что все точки, которые находятся левее или равны , а также все точки, которые находятся правее или равны , удовлетворяют данному условию. Таким образом, множество решений: .
в) Условие означает, что расстояние от точки до точки меньше двух. Это значит, что точки должны находиться внутри интервала, центр которого , а радиус . Следовательно, множество всех таких будет .
г) Условие означает, что расстояние от точки до точки больше двух. Таким образом, рассматриваются все точки, которые удалены от более чем на две единицы. То есть это все точки левее или равные , а также все точки правее или равные . Ответ: .
д) Условие означает, что расстояние от точки до нуля не превышает шести. То есть все значения , находящиеся в пределах от до включительно, удовлетворяют этому условию. Таким образом, множество решений: .
е) Условие означает, что расстояние от точки до нуля не меньше трёх. Это значит, что все точки, которые находятся на координатной прямой не ближе чем на три единицы от нуля, входят в решение. То есть это точки левее или равные , а также точки правее или равные . Ответ: .






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!