
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 8 Дорофеев, Суворова — Подробные Ответы
Найдите объединение и пересечение множеств A и B, если:
а) , ;
б) , ;
в) , .
Образец. Пусть , . Тогда ,
(рис. 1.3).
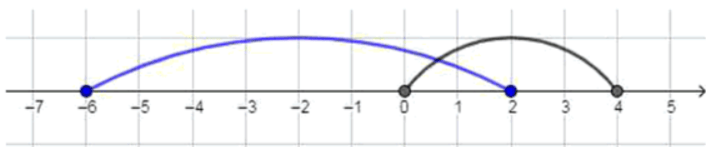
а) Если и :
Объединение множеств определяется как множество всех элементов, которые принадлежат хотя бы одному из множеств или . Интервал охватывает все числа от до включительно, а интервал охватывает все числа от до включительно. При объединении этих интервалов получается один непрерывный интервал от до , то есть .
Пересечение множеств определяется как множество всех элементов, которые одновременно принадлежат и множеству , и множеству . Общая часть интервалов и — это интервал от до , где границы входят, так как в обоих интервалах они включены. Таким образом, .
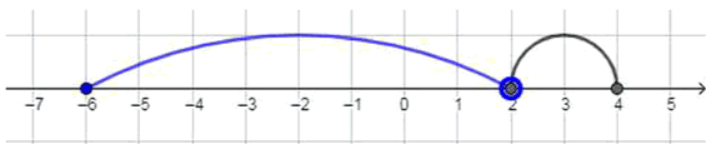
б) Если и :
Объединение охватывает все элементы от до , но не включая , и от до , включая обе границы на второй части. При объединении эти два интервала соединяются в один непрерывный отрезок от до , так как точка принадлежит множеству . В итоге получается .
Пересечение — это множество всех общих элементов интервалов. Интервал содержит числа до , не включая , а интервал начинается с . Таким образом, ни одного общего числа у этих двух множеств нет. Следовательно, .
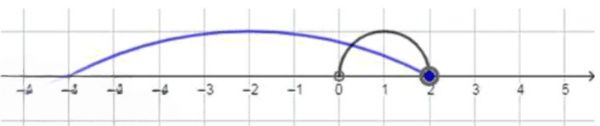
в) Если и :
Объединение включает все элементы интервала , а также интервала . Поскольку полностью содержится в интервале , то при объединении ничего нового не добавляется. Следовательно, .
Пересечение — это общая часть двух интервалов. Интервал включает все числа от до , а интервал включает только числа от до , не включая и . Общая часть этих интервалов — это интервал . Таким образом, .
Итоговые ответы:
а) , ;
б) , ;
в) , .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!